《微观经济学：现代观点》笔记（第一部分：消费者理论・上）

1 市场

1.1 市场均衡

保留价格 某人愿意为某商品支付的最高价格，称为此人的保留价格。换言之，一个人的保留价格是他买或不买该商品的价格临界值。

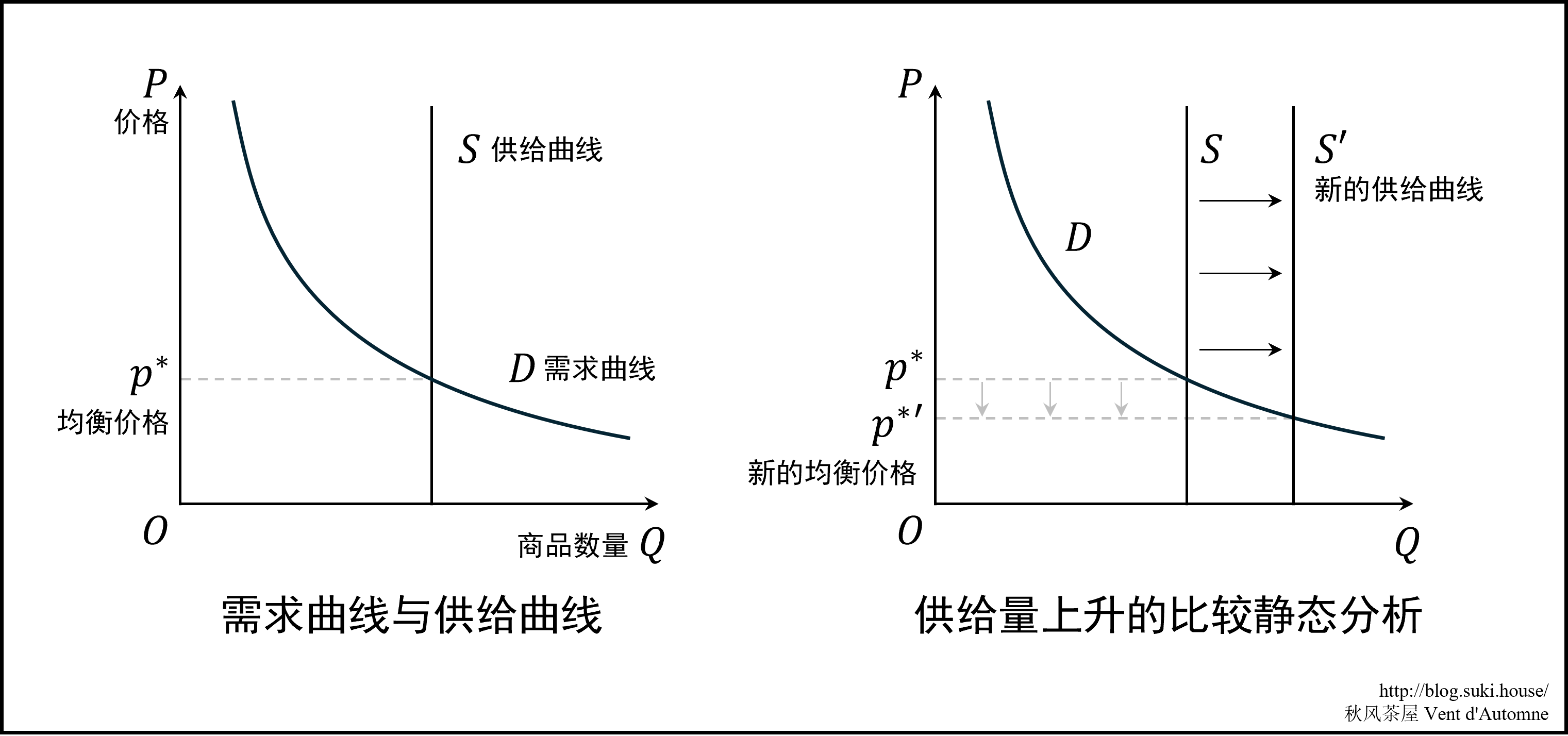
需求曲线与供给曲线 考虑一个坐标轴，纵轴是商品价格 $P$、横轴是商品数量 $Q$。需求曲线 $D$ 表示每一个价格下全体消费者愿意购买的商品数量，它一般是一条下降曲线。在同一时间内，市场上该商品的供应量是不变的，供给曲线 $S$ 是一条垂直线。

市场均衡 当需求量与供给量相同（图像上表现为需求曲线与供给曲线的交点）时，市场是均衡的。此时的商品价格称为均衡价格 $p^*$。

比较静态分析 探讨市场各个方面变化时，商品价格会有什么变动。这种方法称为比较静态分析，因为它关注变化前和变化后两个静态状态并进行比较。例如供给上升时，供给曲线右移，均衡价格向下移动。

1.2 配置住房的方法

  本章以美国中西部一个中等大小城市的大学租房市场为例，该城市分内外两城：内城区房子较近，但价格昂贵；外城区较远，但价格低廉。本章关注内城区房子的价格。本章提出了四种配置住房的方法：

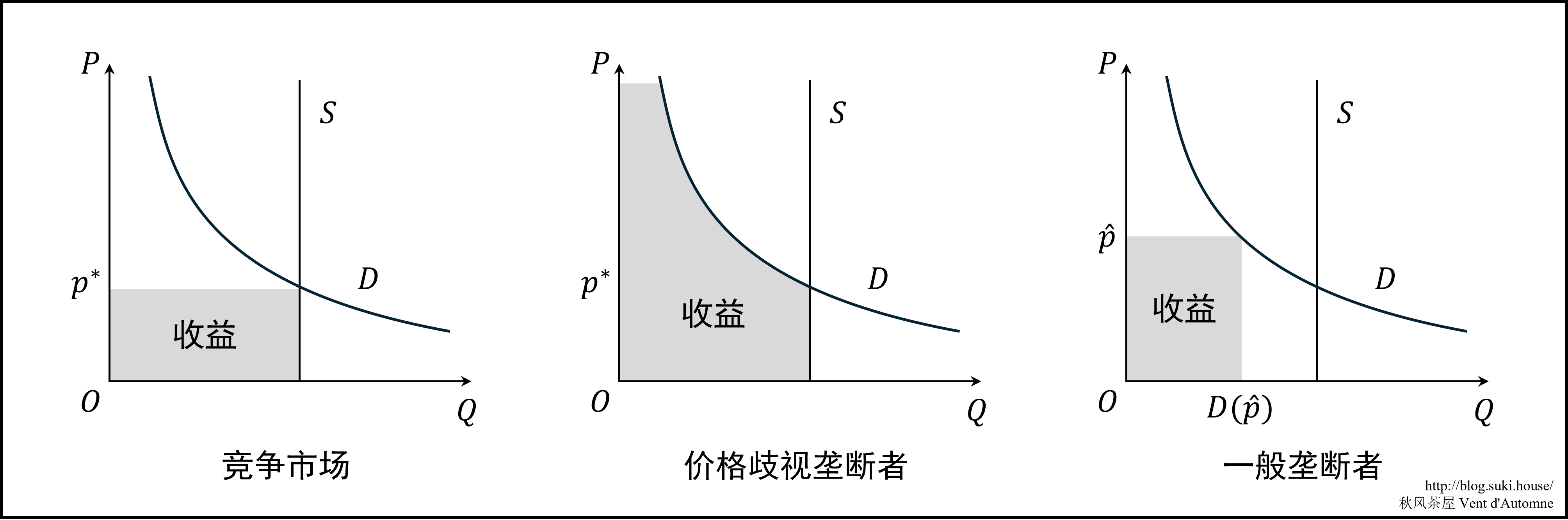
竞争市场 即上文所写的自然的市场均衡，均衡价格位于供给曲线与需求曲线的交点。

价格歧视垄断者 只有一个房东（或房东联盟）拥有所有的住房。假设房东知道每一名学生对住房的保留价格，就可以按照保留价格从高到低依次向学生出租房子。这样每位学生租到的房屋价格是不同的。

一般垄断者 唯一的房东（或房东联盟）被迫按同样价格出租房子时，他需要最大化总收益 $pD(p)$。此时的价格为垄断价格 $\hat p$，总收益 $\hat pD(\hat p)$ 表现为图中灰色方形面积。垄断者出租较少的住房，而每一套住房价格都会高于竞争市场的价格。

房租管制 市议会限制了房租的最高价格 $p_max$，且这个价格小于均衡价格 $p^*$。此时会出现超额需求，愿意租房的学生多于可供应的住房。

1.3 帕累托效率

帕累托效率 如果可以找到一种配置方法，能在不损害其他人利益的情况下将一些人的境况变得好一些，则称它是一个帕累托改进。若一种配置方法存在帕累托改进，则称它是帕累托低效的；反之称它是帕累托高效的。

  例如假设 A 得到一套内城区住房，他的保留价格是 200 美元。B 得到一套外城区住房。再假设 B 愿意用 300 美元去换 A 的住房。现在 B 得到了他认为与 30 美元一样值的住房，A 得到了他认为比住房更值的 300 美元。这是一种帕累托改进。

  竞争市场和价格歧视垄断者都是帕累托高效的。因为它们将住房配置给 $S$ 个持最高保留价格的人，没有更多交易可以进行。

  一般垄断者是帕累托低效的，因为房东可以将剩余房屋出租给保留价格较低的学生——只是“被迫按相同价格出租房子”这一条规则不允许，迫使它变得帕累托低效。

  房租管制是帕累托低效的，它的帕累托改进方法与上文的例子是相同的。

2 预算约束

2.1 预算集

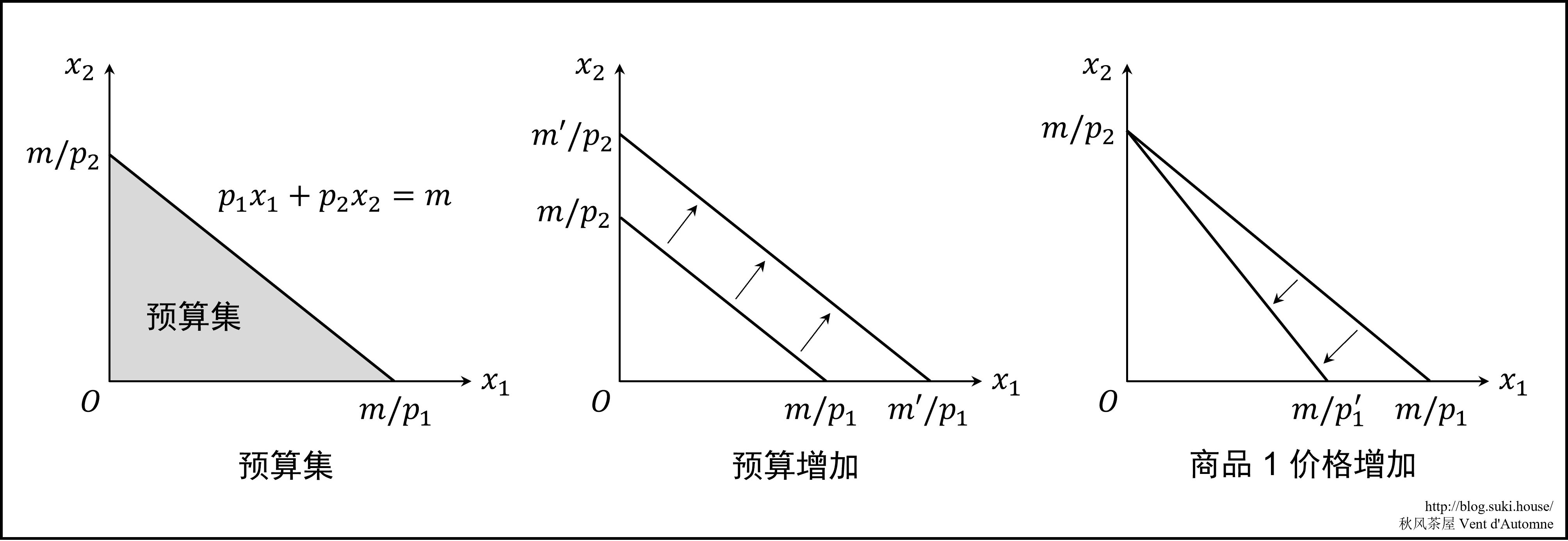
消费束与预算集 假设有两种商品，价格分别为 $(p_1,p_2)$。假设消费者对于这两种商品的购买数量分别为 $(x_1,x_2)$（称为消费束）。假设消费者的最高预算是 $m$。则消费者的预算约束可以写为

$$p_1x_1 + p_2x_2 \leq m$$

所有满足以上不等式的消费束 $(x_1,x_2)$ 称为该消费者的预算集。

通常只考虑两种商品 例如我们研究消费者对牛奶的需求。用 $x_1$ 衡量他每月消费牛奶数量，$p_1$ 为牛奶单价；把商品 2 看作消费者用来购买其它商品的货币，价格是 $1$。约束预算公式可以写作

$$p_1x_1 + x_2 \leq m$$

我们认为商品 2 代表一种符合商品，表示牛奶除外的一切商品。

预算线的性质 预算线是指费用等于预算 $m$ 的一系列消费束，即

$$p_1x_1 + p_2x_2 = m$$

它的横截距是 $m/p_1$，纵截距是 $m/p_2$，斜率是 $-p_1/p_2$。这个斜率的绝对值表示商品 1 来“替代”商品 2 的比率，即为了多购买一个商品 1，消费者需要放弃多少个商品 2.

预算线如何变动 预算增加时，预算线向外平移，截距改变而斜率不变。商品 1 的价格增加时，纵截距不变而斜率变得陡峭，因为商品 1 与商品 2 的价格比率 $p_1/p_2$ 变大。

计价物 可以把预算线方程两侧同除以 $p_2$，得到

$$\frac{p_1}{p_2}x_1 + x_2 = \frac{m}{p_2}$$

等价于将商品 2 价格固定为 $1$，商品 1 的价格和预算金额调整为相对商品 2 价格的比值。此时称商品 2 为计价物。当然也可以同除以 $m$，得到

$$\frac{p_1}{m}x_1 + \frac{p_2}{m}x_2 = 1$$

此时预算是计价物，商品的价格调整为相对预算金额的比值。

2.2 税收、补贴和配给

税收对预算线的影响 税收等价于提高价格。

• 从量税即每购买一件商品需支付一定的税额（设为 $t$），等价于商品价格从 $p_1$ 变为了 $p_1+t$；
• 从价税即购买商品时按总价格的百分比（设为 $\tau$）征税，等价于商品价格变为了 $(1+\tau)p_1$；
• 总额税即不管消费多少商品都征收固定税额（设为 $T$），等价于预算从 $m$ 变为了 $m-T$。

补贴对预算线的影响 补贴等价于降低价格。与税收相同，

• 从量补贴（$s$）按商品数计算，等价于商品价格变为 $p_1-s$；
• 从价补贴（设为 $\sigma$）按总价格计算，等价于商品价格变为 $(1-\sigma)p_1$；
• 总额补贴是不管购买数量的固定征税（设为 $S$），等价于预算变为 $m-S$。

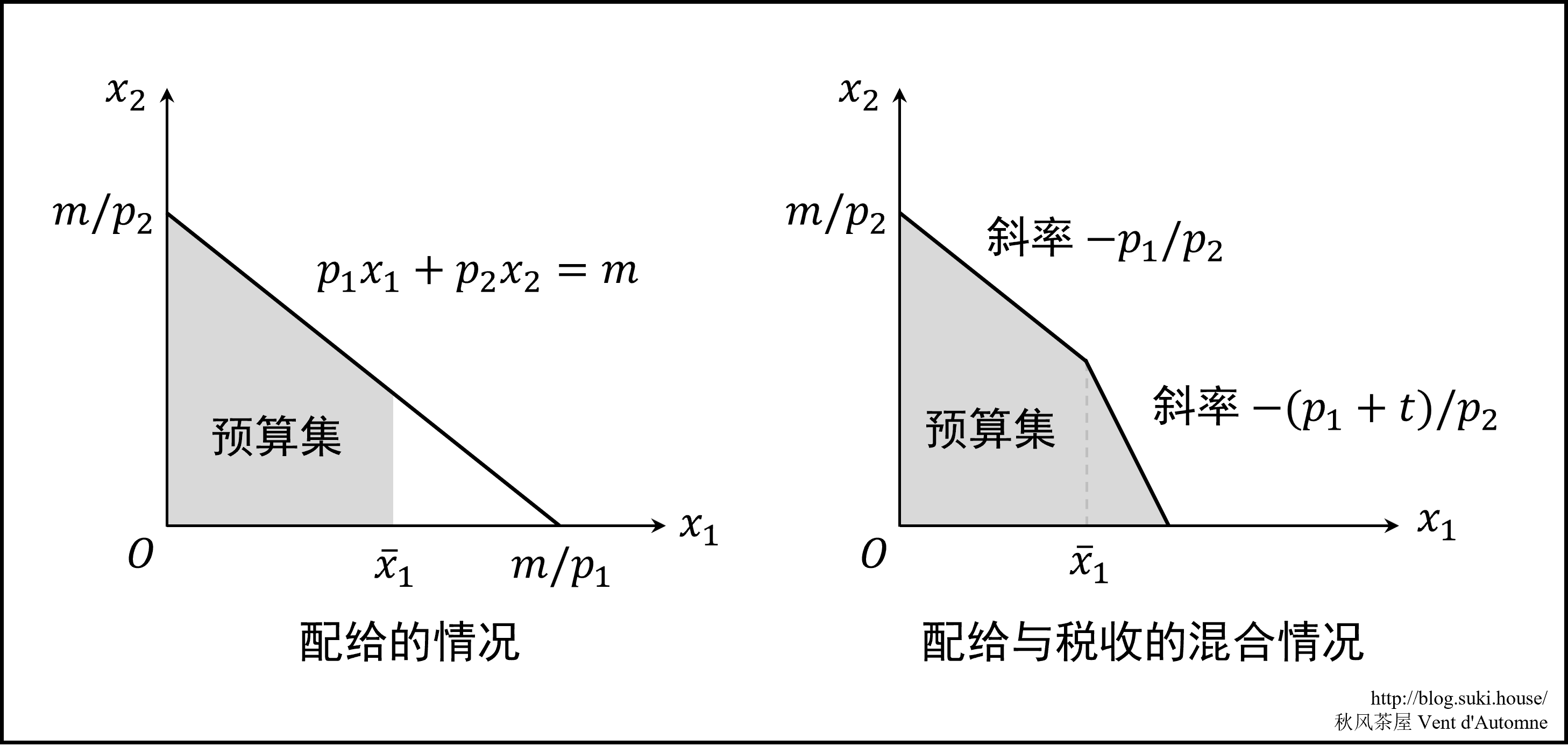
配给对预算线的影响 配给供应即限制消费者购买商品数量不得多于一个固定数（设为 $\bar x_1$）。此时预算集新增一个约束 $x_1\leq\bar x_1$，在图像上表示为预算集被切除了一块。

税收补贴配给的混合情况 考虑阶段性税收：消费者最多可以消费 $\bar x_1$ 件商品 1，超出的部分需要支付从量税 $t$。此时预算集由一个凸四边形构成。

3 偏好

3.1 偏好的定义

偏好的定义 对于消费束 $X=(x_1,x_2)$ 和 $Y=(y_1,y_2)$，消费者可以按照自身偏好对其排序。

• 若消费者总更愿意选择 $X$ 而不是 $Y$，则称 $X$ 严格偏好于 $Y$，记作 $X\succ Y$；
• 若二者皆可，则称 $X$ 与 $Y$ 无差异，记作 $X\sim Y$；
• 若 $X\succ Y$ 或 $X\sim Y$，则称 $X$ 弱偏好于 $Y$，记作 $X\succeq Y$。

弱偏好的公理 弱偏好 $\succeq$ 是一个关系，它由以下三条公理定义：

• 完备性：$\forall X\forall Y, (X\succeq Y)\lor(Y\succeq X)=\top$；
• 反身性：$\forall X, X\succeq X$；
• 传递性：$\forall X\forall Y\forall Z, (X\succeq Y)\land(Y\succeq Z)\implies(X\succeq Z)$。

无差异曲线 $x_1Ox_2$ 坐标平面上的一系列无差异消费束的集合构成一条条无差异曲线，它是一系列等高线，不能相交。箭头指向偏好增加的方向。

3.2 偏好的几个例子

完全替代品 两种商品的总和越多越好，而不管具体是商品 1 还是商品 2。这种情况下无差异曲线在数学上表示为

$$x_1 + x_2 = \text{const}$$

这种情况下所有无差异曲线都有一个不变的斜率 $-1$。

完全互补品 完全互补品是始终以固定比例一起消费的商品，例如左鞋和右鞋。以按 $1:1$ 互补为例，此时偏好取决于两种商品中较少的那一个的数量。这种情况下无差异曲线在数学上表示为

$$\min(x_1, x_2) = \text{const}$$

这种情况下所有无差异曲线都呈平行的 L 形。

厌恶品 有时畅销商品（如烤鸭）会与滞销商品（如鸭脖）捆绑销售。当消费者购买烤鸭时，会按比例捆绑销售一些鸭脖。有一些消费者厌恶鸭脖，此时鸭脖是厌恶品：烤鸭数量一定时，鸭脖数量越多，偏好反而会越低。这种情况下无差异曲线会有正的斜率。

中性商品 有一些消费者对鸭脖的数量完全不在乎，此时鸭脖是中性商品：鸭脖的数量对偏好没有影响。这种情况下无差异曲线是垂直线。

餍 足 有时消费者有一个最佳的消费束（称为餍足点），就偏好而言越接近这个消费束越好。例如这两种商品是巧克力蛋糕和冰淇淋，太少或者过多都会让消费者不舒服。这种情况下无差异曲线围绕着餍足点。

3.3 良态偏好

  本系列重点研究少数几种简单的、一般的、常见的、概括性的无差异曲线，他们有以下特征：

偏好的单调性 即商品多多益善。若 $(x_1,x_2)$ 是一组消费束，消费束 $(y_1,y_2)$ 是一个至少包含相同数量商品并且其中一种商品多一些的消费束，那么 $Y$ 严格偏好于 $X$。用数学语言描述就是

$$\forall X\forall Y, (y_1>x_1)\lor(y_2>x_2)\implies Y\succ X$$

单调性意味着无差异曲线的斜率是负的。某一消费束右上方的消费束必是更偏好的消费束。

偏好的凸性 在任意无差异曲线上取一条割线，割线内部每一消费束均弱偏好于端点

$$\forall X,\forall Y\sim X,\forall t\in[0,1],(tx_1+(1-t)y_1,tx_2+(1-t)y_2)\succeq(x_1,x_2)$$

以冰淇淋和橄榄为例，在一个月内，消费者更愿意吃一些冰淇淋和一些橄榄，而不是在整个月内专门消费其中一种商品。此时无差异曲线是凸（凸向原点）的。

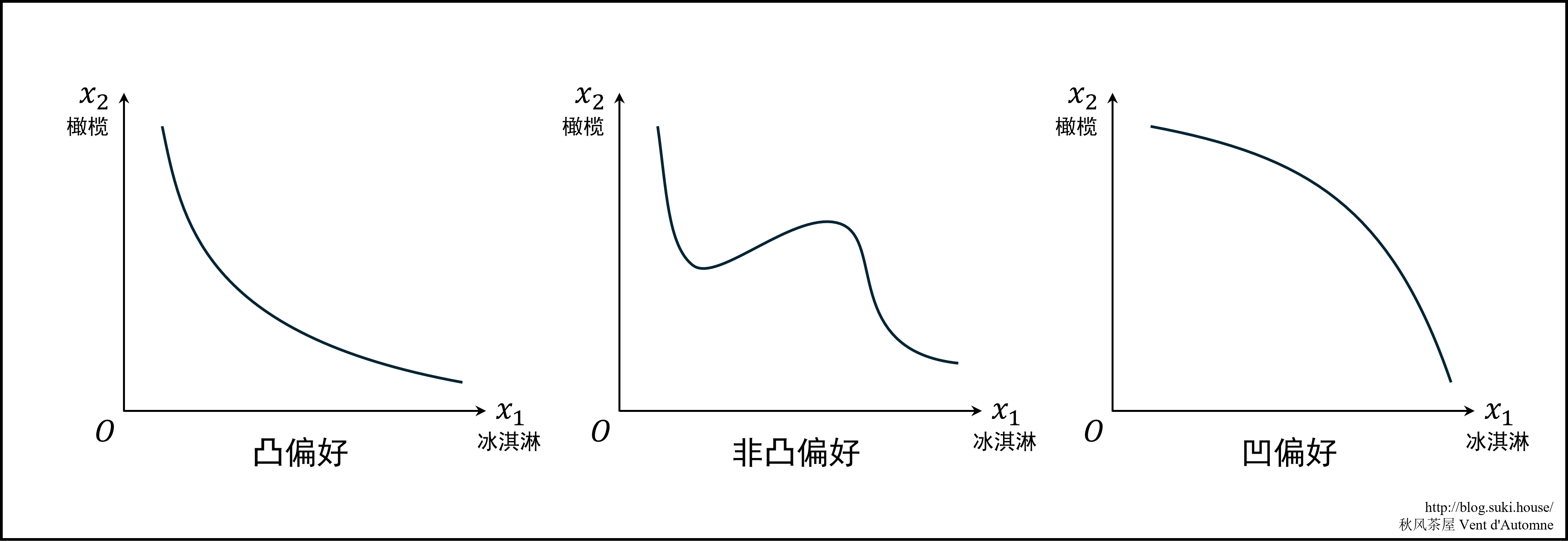
  单调的和凸的偏好称为良态偏好。

  无差异曲线有时也可以是凹的。消费者喜爱冰淇淋和橄榄，但是可能不喜欢同时吃这两样东西。例如某消费者在同一小时内的消费：他也许喜欢消费 2 份冰淇淋或 2 份橄榄，但是都比消费 1 份冰淇淋加 1 份橄榄好。此时无差异曲线是凹的。但是凹偏好的情况较少见，本章不考虑。

边际替代率 无差异曲线的斜率的绝对值称为边际替代率（MRS），它代表消费者愿意用商品 1 去替代商品 2 的比率。

4 效用

4.1 效用函数

效用函数 效用函数是消费束到数值的函数 $u(x_1,x_2)$，它是描述偏好的一种方法。消费束 $X$ 偏好于 $Y$ 高当且仅当其效用比 $Y$ 高，即

$$X \succ Y \iff u(X) > u(Y)$$

单调变换不改变效用函数 一个效用函数 $u$ 的单调变换 $f\circ u$ 还是一个效用函数，且与原效用函数代表的偏好相同。

序数效用与基数效用 序数效用仅关注两消费束的效用值哪一个更高；而基数效用对效用的具体数值赋予了重要意义，例如可以定量比较消费束 $X$ 的效用是消费束 $Y$ 的几倍。基数效用并不是描述行为所必需的，所以本章将坚持序数效用的分析框架。

4.2 效用函数的几个例子

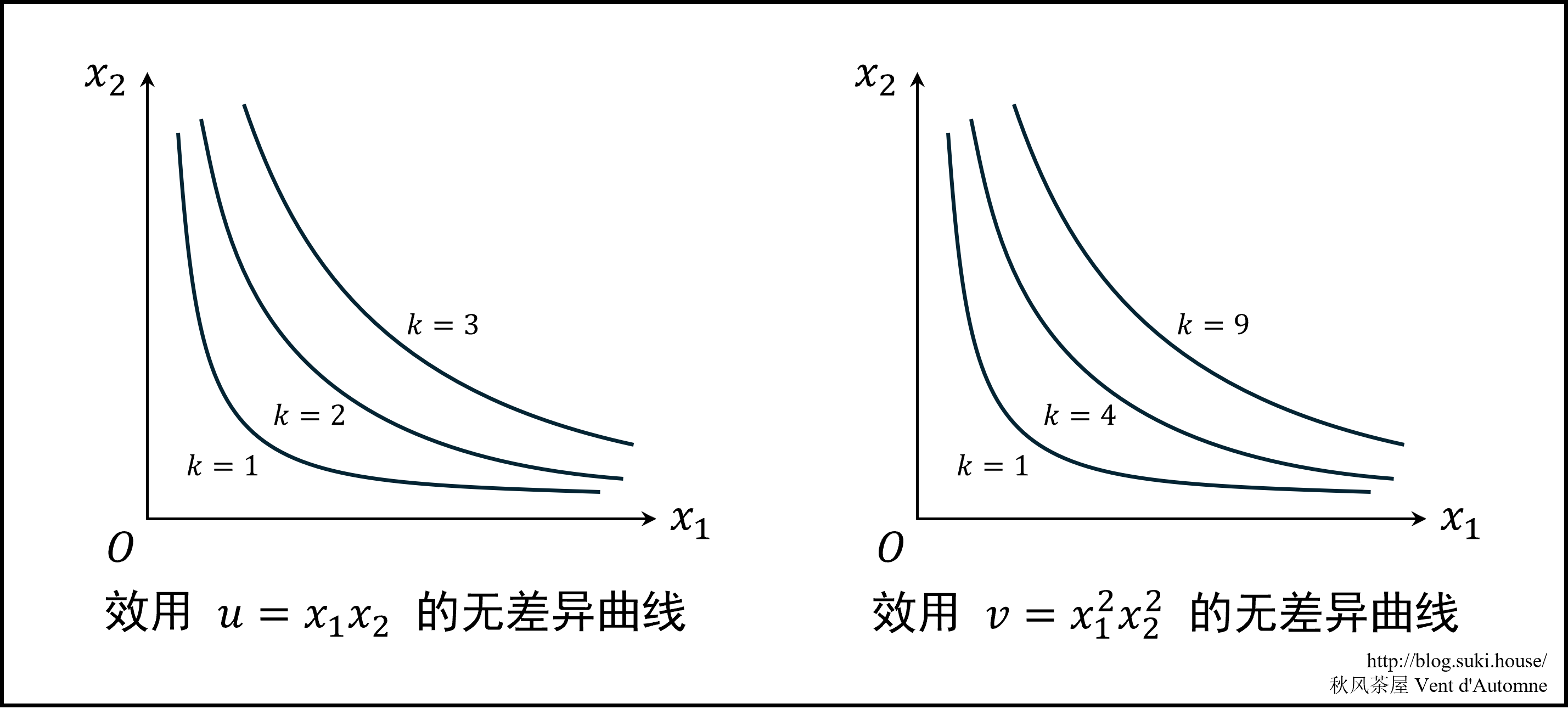
由效用推导出无差异曲线 假设效用函数 $u(x_1,x_2)=x_1x_2$，考察它的无差异曲线

$$u(x_1, x_2) = x_1x_2 = k \iff x_2 = \frac{k}{x_1}$$

这是一系列反比例函数。在考虑效用函数 $v(x_1,x_2)=x_1^2x_2^2$。我们发现

$$v(x_1, x_2) = x_1^2 x_2^2 = u(x_1, x_2) ^2$$

而平方变换在正半轴上是单调变换。所以 $u$ 和 $v$ 的无差异曲线形状完全相同，只是将标号 $1,2,3,\dots$ 换成 $1,4,9,\dots$。他们描述的偏好完全相同。

完全替代 效用仅取决于两商品数量之和，而与每个商品的具体数量无关。一个效用函数是

$$u(x_1, x_2) = x_1 + x_2$$

完全互补 例如左鞋和右鞋。消费者只关心他有多少双鞋，效用函数的值取决于他可以配对鞋子的数量。一个效用函数是

$$u(x_1, x_2) = \min(x_1, x_2)$$

拟线性偏好 拟线性偏好的效用函数是

$$u(x_1, x_2) = v(x_1) + x_2$$

它的无差异曲线是

$$x_2 = -v(x_1) + k$$

即无差异曲线是一条曲线 $x_2=-v(x_1)$ 垂直平移的结果。

柯布—道格拉斯偏好 柯布—道格拉斯偏好的效用函数是

$$u(x_1, x_2) = x_1^c x_2^d$$

其中 $c>0,d>0$ 是参数。两边取对数，效用函数可以写成对数形式

$$v(x_1, x_2) := \ln u = c\ln x_1 + d\ln x_2$$

或者两边同取 $1/(c+d)$ 次幂，就可以减少一个参数

$$w(x_1, x_2) := u^{\frac{1}{c+d}} = x_1^{\frac{c}{c+d}} x_2^{\frac{d}{c+d}} \xlongequal{a:=\frac{c}{c+d}} x_1^a x_2^{1-a}$$

4.3 边际替代率

边际效用 考虑增加一点商品 1 对消费者效用的影响。效用对商品 1 数量的偏导数称作商品 1 的边际效用：

$$MU_1 := \frac{\partial u}{\partial x_1} = \lim _{\Delta x_1 \to 0} \frac{u(x_1 + \Delta x_1, x_2) - u(x_1, x_2)}{\Delta x_1}$$

商品 2 的边际效用 $MU_2$ 是类似的。

边际替代率 边际替代率（MRS）是消费者愿意用商品 2 代替商品 1 的比率。即保持效用 $u$ 不变，为了增加 $1$ 件商品 1，消费者愿意放弃多少件商品 2。假设两件商品的变化量是 $(\mathrm dx_1, \mathrm dx_2)$，则有

$$\mathrm du = \frac{\partial u}{\partial x_1} \mathrm dx_1 + \frac{\partial u}{\partial x_2} \mathrm dx_2$$

函数值为定值即全微分为零，所以

$$\mathrm du = 0 \implies {\rm MRS} := \frac{\mathrm dx_2}{\mathrm dx_1} = -\frac{\partial u}{\partial x_1} \Big/ \frac{\partial u}{\partial x_2} = -\frac{MU_1}{MU_2}$$

注意微分的下标和边际效用的下标是相反的。

边际替代率与调用的表示方法无关 上文提到，相差一个单调变换的效用是同一个效用。虽然变换前后的边际效用不同，但是边际替代率相同。这是因为设 $f$ 是单调变换且 $v=f(u)$，则有

$${\rm MRS} = -\frac{\partial v}{\partial x_1} \Big/ \frac{\partial v}{\partial x_2} = -\left(\frac{\partial f}{\partial u} \cdot \frac{\partial u}{\partial x_1}\right) \Big/ \left(\frac{\partial f}{\partial u} \cdot \frac{\partial u}{\partial x_2}\right) = -\frac{\partial u}{\partial x_1} \Big/ \frac{\partial u}{\partial x_2}$$

  一座城市内往返住所和上班地点的人们都面临着乘公交车还是驾车上班的选择。每一种通勤途径可以提取若干特征（如行车时间、等候时间、费用、舒适度、便利度等）。

  如果要定量描述每种交通方式的效用（可以理解为总评分），可以为每一维特征打一个分 $x_i$，然后分别乘以人们普遍对这一维特征的看重程度 $\beta_i$（根据这一维是正面的还是负面的给出正负号）作为系数。即

$$u(x_1, \dots, x_n) = \pm \beta_1x_1 \pm \dots \pm \beta_nx_n$$

  1967 年的一份研究报告给出了这样的效用函数来描述各交通方式的效用（总评分）：

$$U = -0.147TW - 0.0411TT - 2.24C$$

其中 $TW$ 和 $TT$ 分别表示该种通勤途径的步行时间和行车时间（以分钟计）；$C$ 表示全部费用（以美元计）。系数是通过调查统计得出的。

  这是一个线性模型，各种特征的系数就是其边际效用，系数的比率代表特征之间的边际替代率。步行时间对行车时间的比率大概是 $3:1$，表示人们为了减少 $1$ 分钟步行时间，宁愿增加 $3$ 分钟乘车时间。

  另外注意到行车时间对花费的比率是 $0.0183$，即是说人们愿意花 $0.0183$ 美元去换取减少一分钟通勤时间。这可以为公交车定价提供参考，以确定这些服务是否能收回成本。

5 选择

5.1 最优选择

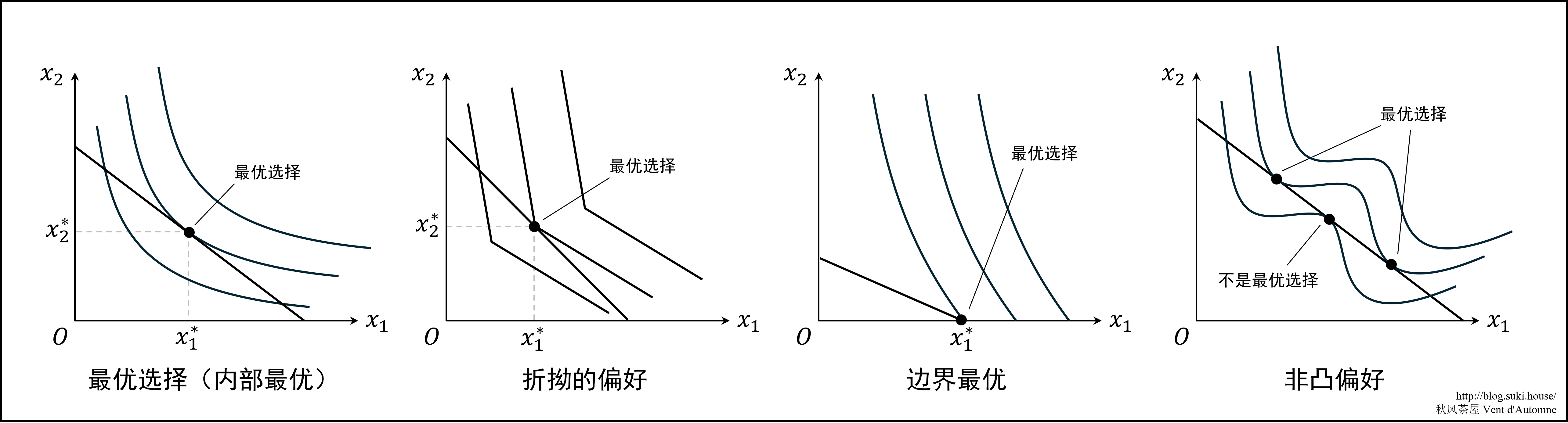
最优选择 消费者总是从他们的预算集中选择最偏好的消费束，称作最优选择。将预算线与无差异曲线绘制在同一个 $x_1Ox_2$ 平面上，最优选择位于预算线与最高的那一条无差异曲线的交点处。

最优选择与切点 如果可能，最优选择一定位于预算线和无差异曲线的切点处。此时无差异曲线的斜率（边际替代率）等于预算线的斜率（商品价格比率），即

$${\rm MRS} = -\frac{p_1}{p_2}$$

  从经济学上理解，如果边际替代率和价格比率不同，例如，假定 ${\rm MRS}=-1/2$，而价格比率为 $1:1$，这意味着消费者愿意放弃两件商品 1 获得一件商品 2，但市场却愿意在 $1:1$ 的基础上交换它们。因此消费者肯定愿意少购买两件商品 1 而多购买一件商品 2。

  在本例中，商品 2 在消费者心目中的“身价”是商品 1 的两倍，而市场价却只是商品 1 的一倍，所以消费者一定会多购买商品 2。直到商品 2 的“身价”“贬值”至只有商品 1 的一倍。

  一般来说切点与最优选择总是绑定出现，但是也有一些例外：

折拗的情况 有时预算线会出现折拗点（不可导点），这些折拗点可能会是最优选择出现的地方。

边界最优 有时最优选择出现在某些商品的消费为 $0$ 的时候，在 $x_1Ox_2$ 平面上表示为最优选择位于坐标轴上。

非凸偏好 在偏好非凸的情况下，预算线与无差异曲线会有多个切点。只有部分切点是最优选择。

需求束和需求函数 给定价格和预算下商品 1 和商品 2 的最优选择 $(x_1^*,x_2^*)$ 称作消费者的需求束。换言之，商品的购买数量是价格和预算的函数 $x_1(p_1,p_2,m)$ 和 $x_2(p_1,p_2,m)$，称作需求函数。

5.2 若干例子

  以下研究若干例子下的需求束。

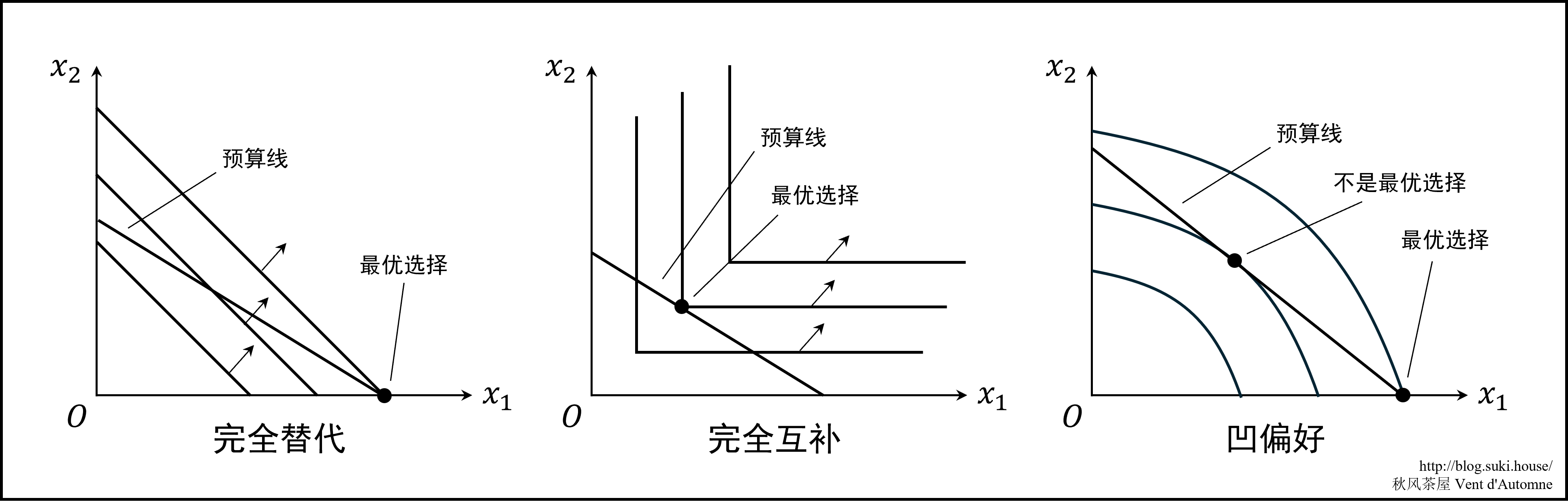
完全替代 假设 $p_1<p_2$，此时预算线的斜率比无差异曲线平坦。预算线与最高的那一条无差异曲线的交点出现在 $x_1$ 轴上，此时

$$x_1^* = m / p_1, \quad x_2^* = 0$$

这与感觉一致，因为在完全替代的情况下，消费者只会购买较便宜的那一种。

完全互补 观察到最优选择总是出现在对角线上。此时

$$x_1 = x_2 = \frac{m}{p_1 + p_2}$$

这是相当直观的：这种消费等价于将所有的钱花费在价格为 $p_1+p_2$ 的单一商品上。

凹偏好 此时切点并不是最优选择，边界上才是。如果你有钱购买冰淇淋和橄榄，而又不喜欢一起消费它们，你就会把钱全部花在其中一种上。

使用拉格朗日乘子法求解需求束 要解决的最优化问题是

$$\begin{aligned} & \max_{(x_1, x_2)} && u(x_1, x_2)\\ & \text{s.t.} && p_1x_1 + p_2x_2 = m \end{aligned}$$

建立辅助函数

$$\mathcal L = u(x_1, x_2) - \lambda(p_1x_1 + p_2x_2 - m)$$

其中 $\lambda$ 是拉格朗日乘子。对 $x_1, x_2, \lambda$ 分别求导并令其为零

$$\left\{ \begin{aligned} & \frac{\partial \mathcal L}{\partial x_1} = \frac{\partial u}{\partial x_1} - \lambda p_1 = 0\\ & \frac{\partial \mathcal L}{\partial x_2} = \frac{\partial u}{\partial x_2} - \lambda p_2 = 0\\ & \frac{\partial \mathcal L}{\partial \lambda} = p_1x_1 + p_2x_2 - m = 0 \end{aligned} \right.$$

柯布—道格拉斯偏好 柯布—道格拉斯函数的对数形式的效用是

$$u(x_1, x_2) = c\ln x_1 + d\ln x_2$$

它的拉格朗日辅助函数是

$$\mathcal L = c\ln x_1 + d\ln x_2 - \lambda(p_1x_1 + p_2x_2 - m)$$

求导并令其为零

$$\left\{ \begin{aligned} & \frac{\partial \mathcal L}{\partial x_1} = \frac{c}{x_1} - \lambda p_1 = 0\\ & \frac{\partial \mathcal L}{\partial x_2} = \frac{d}{x_2} - \lambda p_2 = 0\\ & \frac{\partial \mathcal L}{\partial \lambda} = p_1x_1 + p_2x_2 - m = 0 \end{aligned} \right.$$

求解，可以得到

$$\lambda^* = \frac{c + d}{m}, \qquad x_1^* = \frac{c}{c + d} \cdot \frac{m}{p_1}, \qquad x_2^* = \frac{d}{c + d} \cdot \frac{m}{p_2}$$

  柯布—道格拉斯偏好有一个性质。考察消费者在商品 1 上的花费占它预算的比重

$$a := \frac{p_1x_1^*}{m} = \frac{p_1}{m} \cdot \frac{c}{c + d} \cdot \frac{m}{p_1} = \frac{c}{c + d}$$

因此，具有柯布—道格拉斯偏好的消费者在商品 1 上的花费占它总预算的 $c/(c+d)$ 而与商品价格、预算无关。这就是为什么采用

$$u(x_1, x_2) = x_1^a x_2^{1-a}$$

的形式表示柯布—道格拉斯效用会非常方便的原因。

5.3 税收类型的选择

  从量税是对商品消费量征税，所得税是对收入（预算）征税。如果政府想要增加收入，是征收从量税好还是所得税好呢？

  首先写出原来的预算线

$$p_1x_1 + p_2x_2 = m$$

它的斜率是 $-p_1/p_2$。

  分析从量税。按税率 $t$ 对商品 1 征收从量税，相当于预算线变为

$$(p_1 + t)x_1 + p_2x_2 = m$$

它的斜率是 $-(p_1+t)/p_2$，变得陡峭了。假设征收从量税时，消费者的最优选择是 $(x_1^*,x_2^*)$。它一定位于从量税预算线和无差异曲线的切点。通过从量税，政府获得的收入是 $tx_1^*$。

  考虑使政府获得相同收入所得税的情况。这种情况下的预算线是

$$p_1x_1 + p_2x_2 = m - tx_1^*$$

可以验证它一定过点 $(x_1^*,x_2^*)$，但是它的斜率是 $-p_1/p_2$。可以将从量税的预算线和所得税的预算线画在 $x_1Ox_2$ 平面上。

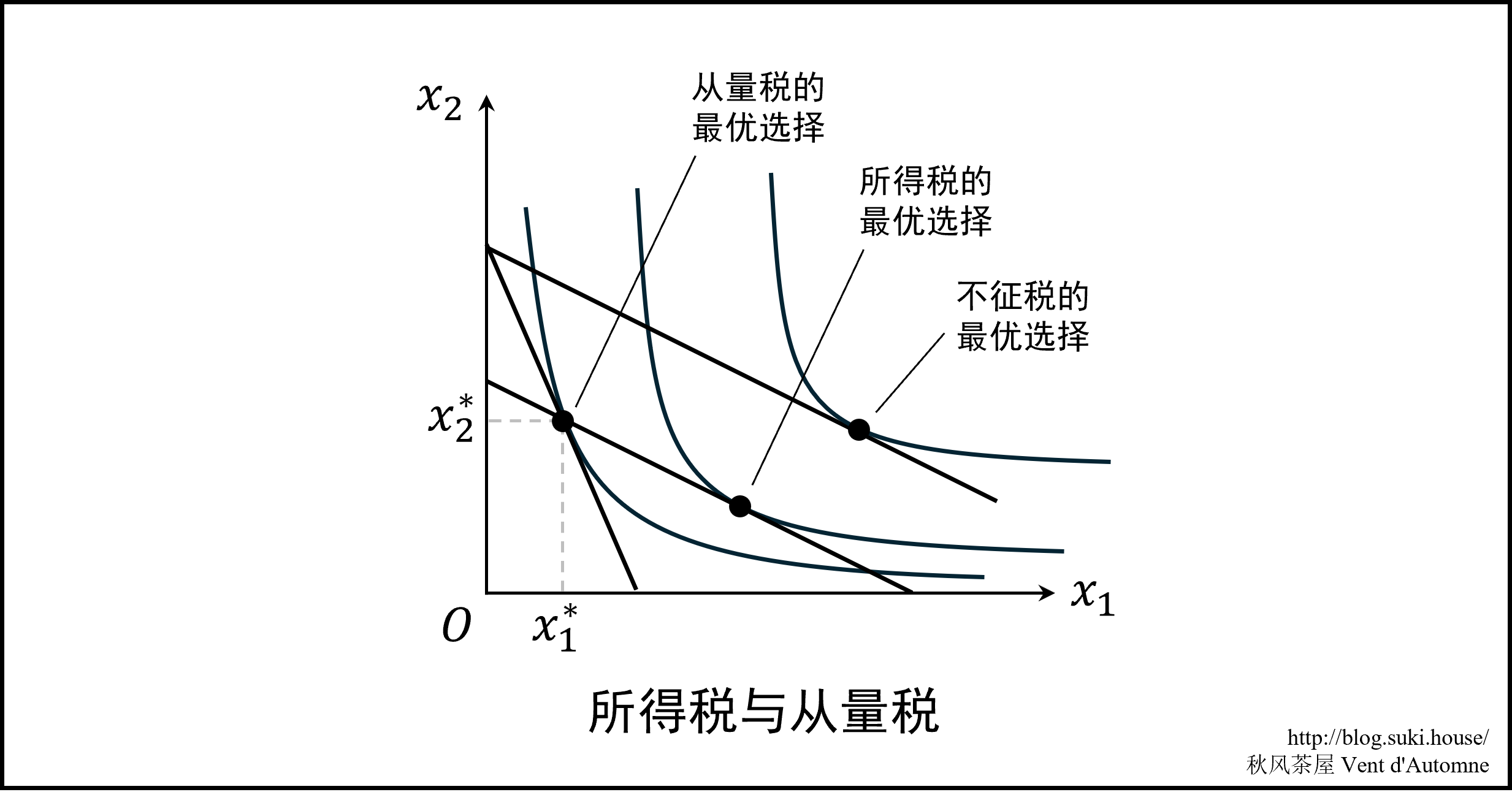
  因此，在政府向消费者征收税额相同的条件下，征收所得税时消费者的境况会比征收从量税时好。从这个意义上说，所得税优于从量税。

本系列的参考文献

[1] 哈尔・R・范里安, 费方域等. 微观经济学: 现代观点[M]. 上海: 格致出版社, 2015.