跳到主要内容

量子力学中的 Dirac 符号

1 对偶空间

向量空间 称三元组 (V,+,⋅)(V, +, \cdot) 为定义在域 FF 上的一个向量空间, 如果

  • (V,+)(V, +) 是 Abel 群;
  • 对 FF 的幺元 11 有 ∀α∈V,1α=α\forall \alpha \in V, 1\alpha = \alpha;
  • 结合律: ∀k,ℓ∈F,∀α∈V,(kℓ)α=k(ℓα)\forall k, \ell \in F, \forall \alpha \in V, (k\ell)\alpha = k(\ell \alpha);
  • 分配律:
    • ∀k,ℓ∈F,∀α∈V,(k+ℓ)α=kα+ℓα\forall k, \ell \in F, \forall \alpha \in V, (k + \ell)\alpha = k\alpha + \ell \alpha;
    • ∀k∈F,∀α,β∈V,k(α+β)=kα+kβ\forall k \in F, \forall \alpha, \beta \in V, k(\alpha + \beta) = k\alpha + k\beta.

线性函数 若函数 f:V→Ff:V \to F 使得 ∀k∈F,∀α,β∈V\forall k \in F, \forall \alpha, \beta \in V,

f(α+β)=f(α)+f(β),f(kα)=kf(α)f(\alpha + \beta) = f(\alpha) + f(\beta), \quad f(k\alpha) = kf(\alpha)

则称 ff 是 VV 上的一个线性函数.

对偶空间 本文假设 dim⁡V<∞\dim V < \infty. 向量空间 VV 上所有线性函数构成的集合称为 VV 的对偶空间, 记为 V∗V^*. 定义线性函数的加法与数乘: ∀k∈F,∀f,g∈V∗,∀α∈V\forall k \in F, \forall f, g \in V^*, \forall \alpha \in V,

(f+g)(α):=f(α)+g(α),(kf)(α):=kf(α)(f + g)(\alpha) := f(\alpha) + g(\alpha), \quad (kf)(\alpha) := kf(\alpha)

此时 V∗V^* 也是一个向量空间. 请注意, 线性函数对向量进行操作 f(α)f(\alpha) 也可以看成线性函数在与向量作纯量积 (f,α)(f, \alpha), 这指明了这是一个 V∗×V→FV^* \times V \to F 的线性映射.

对偶基 设 e1,…,ene_1, \dots, e_n 是 VV 的一组基, 称 V∗V^* 的基 e(1),…,e(n)e^{(1)}, \dots, e^{(n)} 是 e1,…,ene_1, \dots, e_n 的对偶基, 如果 e(i)(ej)=1i=je^{(i)}(e_j) = \mathit 1_{i = j}

例 C3\mathbb C^3 是 C\mathbb C 上的一个向量空间, 它由全体列向量 x=(x1,x2,x3)H\boldsymbol x = (x_1, x_2, x_3)^H 构成, 它有基

e1=(1,0,0)H,e2=(0,1,0)H,e3=(0,0,1)H\boldsymbol e_1 = (1, 0, 0)^H, \quad \boldsymbol e_2 = (0, 1, 0)^H, \quad \boldsymbol e_3 = (0, 0, 1)^H

  考虑由向量 x∈C3\boldsymbol x \in \mathbb C^3 诱导的函数 fx:C3→Cf_{\boldsymbol x}: \mathbb C^3 \to \mathbb C,

fx(y)=x1y1+x2y2+x3y3=xHyf_{\boldsymbol x}(\boldsymbol y) = x_1y_1 + x_2y_2 + x_3y_3 = \boldsymbol x^H\boldsymbol y

所有 C3\mathbb C^3 内的向量诱导出的函数的集合构成了 C3\mathbb C^3 的对偶空间. 它的对偶基是

e(1)(x)=(1,0,0)x,e(2)(x)=(0,1,0)x,e(3)(x)=(0,0,1)xe^{(1)}(\boldsymbol x) = (1, 0, 0)\boldsymbol x, \quad e^{(2)}(\boldsymbol x) = (0, 1, 0)\boldsymbol x, \quad e^{(3)}(\boldsymbol x) = (0, 0, 1)\boldsymbol x

对偶空间 C3∗{\mathbb C^3}^* 上所有元素均可以写成对偶基的线性组合:

fx(⋅)=x1e(1)(⋅)+x2e(2)(⋅)+x3e(3)(⋅)f_{\boldsymbol x}(\cdot) = x_1e^{(1)}(\cdot) + x_2e^{(2)}(\cdot) + x_3e^{(3)}(\cdot)

对偶空间 C3∗{\mathbb C^3}^* 与行向量 x=(x1,x2,x3)\boldsymbol x = (x_1, x_2, x_3) 形成了一一对应. 我们可以认为列向量 C3\mathbb C^3 的对偶空间是行向量 C1×3\mathbb C^{1 \times 3}.

  请注意这里 (cx)H=cˉxH(c\boldsymbol x)^H=\bar c\boldsymbol x^H 需要取共轭.

例 在 C3\mathbb C^3 上的任意一组基 a,b,c\boldsymbol a, \boldsymbol b, \boldsymbol c, 我们可以定义它的对偶基

fa(x)=b×cΩ⋅x,fb(x)=c×aΩ⋅x,fc(x)=a×bΩ⋅xf_{\boldsymbol a}(\boldsymbol x) = \frac{\boldsymbol b \times \boldsymbol c}{\Omega} \cdot \boldsymbol x, \quad f_{\boldsymbol b}(\boldsymbol x) = \frac{\boldsymbol c \times \boldsymbol a}{\Omega} \cdot \boldsymbol x, \quad f_{\boldsymbol c}(\boldsymbol x) = \frac{\boldsymbol a \times \boldsymbol b}{\Omega} \cdot \boldsymbol x

其中 Ω=a⋅(b×c)\Omega = \boldsymbol a \cdot(\boldsymbol b \times \boldsymbol c).

2 算符

算符 向量空间 VV 上的一个算符 AA 是指其自身上的一个映射 A:V→VA:V \to V.

对偶算符 假设 VV 到 V∗V^* 存在一个双射 v:V→V∗v:V \to V^*, 向量 f∈Vf \in V 有对应的像 η:=v(f)∈V∗\eta := v(f) \in V^*. 对于算符 A:V→VA:V \to V, 如果有算符 A∗:V∗→V∗A^*:V^* \to V^* 使得

(η,Af)=(A∗η,f)(\eta, Af) = (A^*\eta, f)

从图上理解, 就是两条红虚线产生的纯量积需要相等.

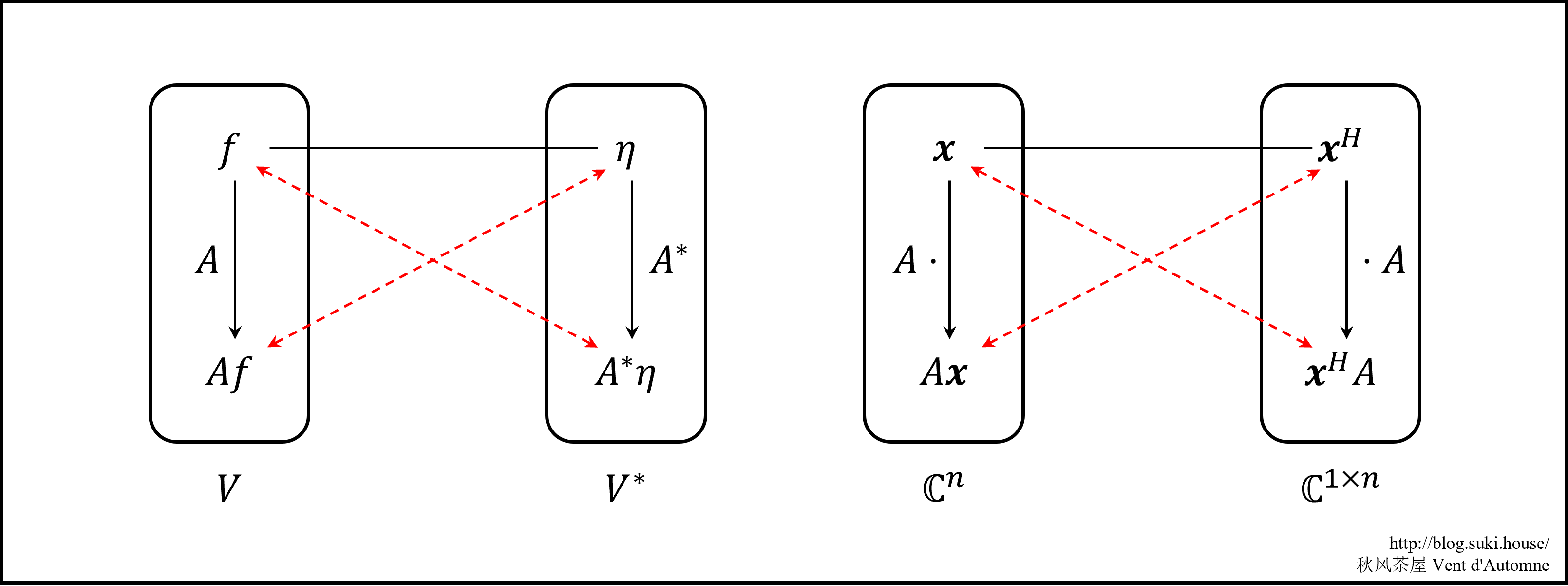
图1: 对偶算符的定义

例 设 V=CnV = \mathbb C^n, V∗=C1×nV^* = \mathbb C^{1 \times n}. VV 上的算符是矩阵 AA 左乘, 可以写成 A⋅A \cdot, 则其对偶算符是矩阵的右乘 ⋅A\cdot A. 此时有

xH(Ax)=(xHA)x=xHAx\boldsymbol x^H(A\boldsymbol x) = (\boldsymbol x^HA)\boldsymbol x = \boldsymbol x^HA \boldsymbol x

伴随算符 向量 ff 依次经过 v,A∗,v−1v, A^*, v^{-1} 之后回到一个 VV 中的向量, 将这个向量定义为 ff 经过 AA 的伴随算符 A†A^\dag 的结果. 即定义

A†=v−1∘A∗∘vA^\dag = v^{-1} \circ A^* \circ v

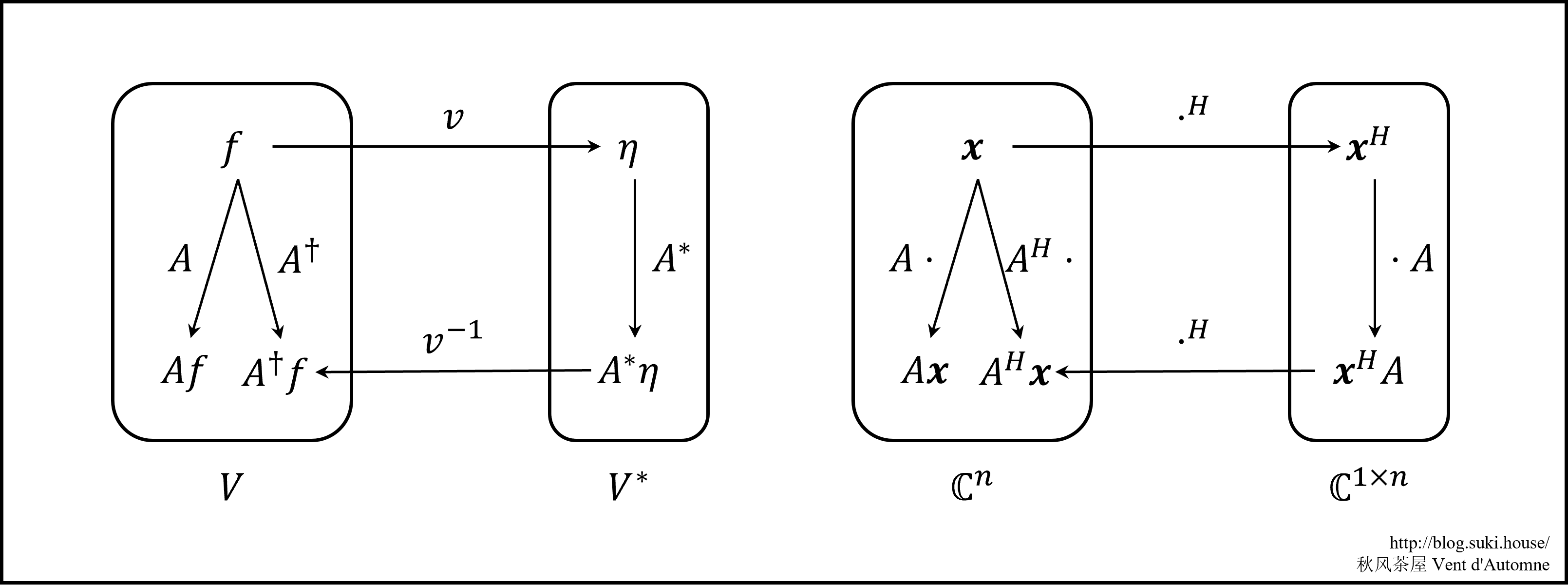
图2: 伴随算符的定义

例 设 V=CnV = \mathbb C^n, V∗=C1×nV^* = \mathbb C^{1 \times n}. A⋅A \cdot 的伴随算符是 AH⋅A^H \cdot, 因为

AHx=(xHA)HA^H\boldsymbol x = (\boldsymbol x^HA)^H

  完善 V∗V^* 一侧的伴随算符, 可以得到完整的结构图.

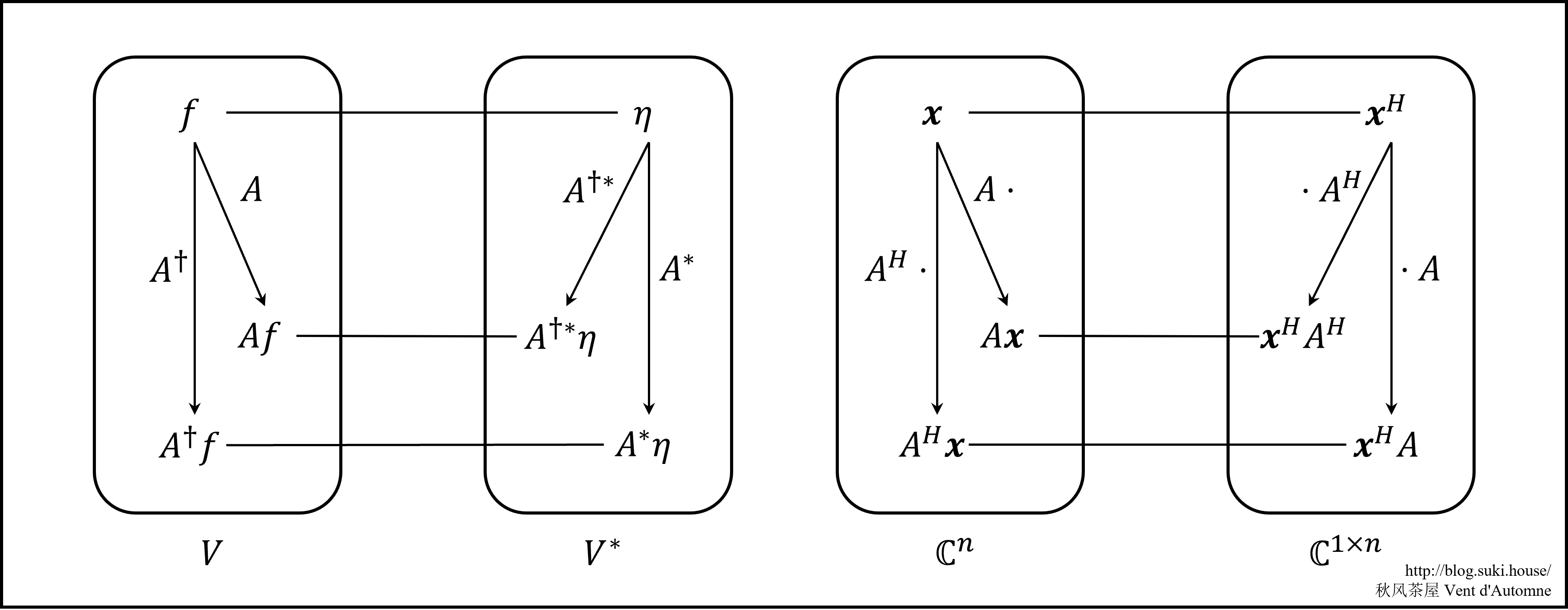
图3: 完整的结构图

3 Dirac 符号

  Dirac 括号是将 VV 中的向量写作右矢 ∣ψ⟩|\psi\rangle, 将 V∗V^* 中的向量写作左矢 ⟨ψ∣\langle\psi| 而得出的一系列符号语言. 以下是它的写法和运算法则与线性代数中法则的对应:

Dirac 符号的语言线性代数的语言说明
∥ψ⟩,⟨ψ∥\|\psi\rangle, \langle\psi\|x,xH\boldsymbol x, \boldsymbol x^H左右矢
A,A∗,A†,A†∗A, A^*, A^\dag, A^{\dag *}A⋅,⋅A,AH⋅,⋅AHA\cdot, \cdot A, A^H\cdot, \cdot A^H算子、对偶、伴随、对偶伴随
⟨ψ∥ϕ⟩\langle\psi\|\phi\ranglexHy\boldsymbol x^H\boldsymbol y纯量积
⟨ψ∥A∥ϕ⟩\langle\psi\|A\|\phi\ranglexHAy\boldsymbol x^HA\boldsymbol y双线性型
∥cψ⟩=c∥ψ⟩\|c\psi\rangle = c\|\psi\rangle(cx)=c(x)(c\boldsymbol x) = c(\boldsymbol x)右矢数乘可以提到括号外
⟨cψ∥=cˉ⟨ψ∥\langle c\psi\| = \bar c\langle\psi\|(cx)H=cˉxH(c\boldsymbol x)^H = \bar c\boldsymbol x^H左矢数乘可以提到括号外, 但是要取共轭
∥Aψ⟩=A∥ψ⟩\|A\psi\rangle = A\|\psi\rangle(Ax)=A(x)(A\boldsymbol x) = A(\boldsymbol x)右矢算符可以提到括号外
⟨Aψ∥=A†∗⟨ψ∥\langle A\psi\| = A^{\dag *}\langle\psi\|(Ax)H=xHAH(A\boldsymbol x)^H = \boldsymbol x^HA^H左矢算符可以提到括号外, 但是要取对偶伴随
⟨ψ∥A=A∗⟨ψ∥\langle\psi\|A = A^*\langle \psi\|xHA⋅=(xHA)⋅\boldsymbol x^HA\cdot = (\boldsymbol x^HA)\cdot左矢后的算符可以提到左矢前, 但是要取对偶
∥ψ⟩‾=⟨ψ∥,⟨ψ∥‾=∥ψ⟩\overline{\|\psi\rangle} = \langle\psi\|, \overline{\langle\psi\|} = \|\psi\rangle(x)H=xH,(xH)H=x(\boldsymbol x)^H = \boldsymbol x^H, (\boldsymbol x^H)^H = \boldsymbol x左右矢的对偶
A∥ψ⟩‾=⟨ψ∥A†\overline{A\|\psi\rangle} = \langle\psi\|A^\dag(Ax)H⋅=xHAH⋅(A\boldsymbol x)^H\cdot = \boldsymbol x^HA^H\cdot左右矢算符的对偶

参考文献

[1] https://www.bilibili.com/video/BV1za4y1F7xo.