线性代数：几何视角与代数视角（一、向量与空间）

1.1 向量及其基本运算

  作为本系列的主要研究对象, 我们先来定义向量.

定义 1.1.1 向量 (Vector) 是有大小、有方向的量.

  习惯上, 我们使用粗体字母 $\boldsymbol a,\ \boldsymbol b$ 等来命名向量. 在不便加粗的场合 (如手写时) 也可以使用带箭头的字母如 $\vec a,\ \vec b$ 等.

注记 1.1.2 大小和方向是向量仅有的两个属性. 我们说两个向量相等, 当且仅当它们的大小相等且方向一致, 而与它们的摆放位置无关. 故为了论述方便, 本系列将所有向量的起点“拖动”到同一个点, 并将其称为原点. 本系列中所有向量的起点均位于原点.

  例如下图中的 $\color{red}{\boldsymbol a}$ 和 $\color{blue}{\boldsymbol b}$ 是平面上两个不相等的向量.

几何视角	代数视角
图1.1.1: 向量是有大小有方向的量	$\color{red}{\boldsymbol a}\neq \color{blue}{\boldsymbol b}$

  现在来定义向量的两个基本运算: 加法和数乘. 本文暂不定义向量的其它运算.

定义 1.1.3 两个向量的和通过如下图所示的平行四边形法则得出.

几何视角	代数视角
图1.1.2: 向量加法的平行四边形法则	$\color{red}{\boldsymbol a}+\color{blue}{\boldsymbol b}=\boldsymbol c$

定义 1.1.4 数与向量的乘积通过如下图所示的伸缩法则得出.

几何视角	代数视角
图1.1.3: 向量数乘就是向量的伸缩	$2\color{red}{\boldsymbol a}=\boldsymbol b$

定义 1.1.5 起点与终点重合的向量称为零向量, 记作 $\boldsymbol 0$ 或 $\vec 0$.

注记 1.1.6 向量可以乘以零. 任何向量乘以零等于零向量. 向量可以乘以负数. 向量乘以负数即是向该向量的镜像方向延伸.

几何视角	代数视角
图1.1.4: 向量乘以负数	$-2\color{red}{\boldsymbol a}=\boldsymbol b$

---

1.2 向量的描述：基与坐标

  我们发现, 仅使用图 1.1 中的两个向量的数乘之和 (即 $k\boldsymbol a+\ell \boldsymbol b$ 的形式) 可以表示平面上的所有向量. 并且对于每个向量, $k$ 和 $\ell$ 的取值是唯一的. 故我们不妨将下图中的向量记作

$$\boldsymbol x=\begin{pmatrix}2\\1\end{pmatrix}$$

几何视角	代数视角
图1.2.1: 用坐标描述向量	$\boldsymbol x=2\color{red}{\boldsymbol a}+1\color{blue}{\boldsymbol b}=\begin{pmatrix}2\\1\end{pmatrix}$

  接下来把上面的例子抽象化, 引出基与坐标的概念.

定义 1.2.1 一个向量组就是一组向量. 一般记作 $A=(\boldsymbol a_1,\boldsymbol a_2,\cdots,\boldsymbol a_n)$. 例如图 1.1 中的两个向量可以构成一个向量组 $A=(\boldsymbol a,\boldsymbol b)$.

定义 1.2.2 对于一个向量组, 若所研究的空间中 (在上例中是平面) 的每一向量, 均可以唯一地表示为该向量组中向量的数乘之和的形式, 则称该向量组是该空间的一组基 (Basis). 基一般用花括号表示, 如 $\{\boldsymbol a\}=\{\boldsymbol a_1,\boldsymbol a_2,\cdots,\boldsymbol a_n\}$.

定义 1.2.3 若一个向量 $\boldsymbol x$ 对于一组基 $\{\boldsymbol a\}$ 有唯一的表示方法 $\boldsymbol x=k_1\boldsymbol a_1+k_2\boldsymbol a_2+\cdots+k_n\boldsymbol a_n$, 则记

$$\boldsymbol x=\begin{pmatrix}k_1\\k_2\\\vdots\\k_n\end{pmatrix}$$

并称其为 $\boldsymbol x$ 在基 $\{\boldsymbol a\}$ 下的坐标 (Coordinates).

记号 1.2.4 为节省版面空间, 上述坐标也可以记作

$$\boldsymbol x=(k_1, k_2, \cdots, k_n)^T$$

其中右上角的 $^T$ 注明了该坐标原本应该是竖向书写的形式.

---

1.3 向量组的线性相关性

  如上节所述, 一组基要是一组良好的基, 必须满足每一向量有唯一的坐标. 在本节中, 我们先来讨论什么样的基是一组良好的基. 下图的基 $\{\color{red}{\boldsymbol a}, \color{blue}{\boldsymbol b}\}$ 就不是一组良好的基, 因为这两个向量共线.

几何视角	代数视角
图1.3.1: 另一组不良好的基	$\color{orange}{\boldsymbol x}=(-2,0)^T=(0,-1)^T$ $\color{purple}{\boldsymbol y}$ 没有对应的坐标表达

注记 1.3.1 上图中的橙色点本应是一个从原点指向该点的箭头, 但是为了图片的简洁清晰, 简写成了一个点的形式. 紫色点同理.

  下图的基 $\{\color{red}{\boldsymbol a}, \color{blue}{\boldsymbol b}, \color{green}{\boldsymbol c}\}$ 也不是一组良好的基, 因为这三个向量共面.

几何视角	代数视角
图1.3.2: 另一组不良好的基	$\color{orange}{\boldsymbol x}=(1,1,0)^T=(0,0,1)^T$ $\color{purple}{\boldsymbol y}$ 没有对应的坐标表达

  现在我们将两向量的共线、三向量的共面推广, 引出一般的 $n$ 个向量下的情况.

定义 1.3.2 称一个向量 $\boldsymbol x$ 是一组向量 $A=(\boldsymbol a_1, \boldsymbol a_2, \cdots, \boldsymbol a_n)$ 的线性组合, 如果这个向量可以表示为这组向量的数乘之和的形式. 即存在一组 $k_1, k_2,\cdots, k_n$ 使得

$$\boldsymbol x=k_1\boldsymbol a_1+k_2\boldsymbol a_2+\cdots+k_n\boldsymbol a_n$$

同时称该向量 $\boldsymbol x$ 能被该向量组 $A$ 线性表出.

例 1.3.3 图 1.3.1 中 $\color{blue}{\boldsymbol b}$ 可以被由一个向量构成的向量组 $(\color{red}{\boldsymbol a})$ 线性表出, $\color{red}{\boldsymbol a}$ 也可以被由一个向量构成的向量组 $(\color{blue}{\boldsymbol b})$ 线性表出. 图 1.3.2 中的三个向量 $\color{red}{\boldsymbol a}, \color{blue}{\boldsymbol b}, \color{green}{\boldsymbol c}$, 每一个都能被其余两个所形成的向量组线性表出.

定义 1.3.4 称一个向量组线性相关 (Linear Dependent), 如果其中至少有一个向量能被其它向量线性表出. 称一个向量组线性无关 (Linear Independent), 如果它不是线性相关的.

例 1.3.5 图 1.3.1 中的向量组 $(\color{red}{\boldsymbol a},\color{blue}{\boldsymbol b})$ 是线性相关的. 图 1.3.2 中向量组 $(\color{red}{\boldsymbol a}, \color{blue}{\boldsymbol b}, \color{green}{\boldsymbol c})$ 也是线性相关的. 但是下图中的向量组 $(\color{red}{\boldsymbol a}, \color{blue}{\boldsymbol b}, \color{green}{\boldsymbol c})$ 是线性无关的.

几何视角	代数视角
图1.3.3: 一组线性无关的向量	-

定理 1.3.6 一个向量组 $A=(\boldsymbol a_1,\boldsymbol a_2,\cdots,\boldsymbol a_n)$ 是线性相关的, 当且仅当方程

$$k_1\boldsymbol a_1+k_2\boldsymbol a_2+\cdots+k_n\boldsymbol a_n=\boldsymbol 0$$

有不全为零的解 (即非零解). 该定理的证明见附录.

推论 1.3.7 一个向量组 $A$ 是线性无关的, 当且仅当方程前述方程只有 $k_1=k_2=\cdots=k_n=0$ 这一个解 (即仅有零解).

---

1.4 向量组张成的空间

  回顾图 1.1.1, 想象这两个向量所有的线性组合. 这两个向量从中心向外张开, 从而可以组合成全平面的向量. 我们说这两个向量可以张成一个平面.

定义 1.4.1 向量组 $A$ 张成的空间即是指 $A$ 中向量所有可能的线性组合的集合. 一个向量组张成的空间可能是一条直线、一个平面、一个立体空间, 也可能是 4 维或以上的空间. 向量组 $A$ 张成的空间记为 $\operatorname{\mathrm{span}} A$.

注记 1.4.2 一个向量组张成的空间必是一个向所有方向延伸的无穷空间. 例如 2 维的张成空间只会是一个平面, 而不会是一个三角形、一个圆, 也不会是 $x$- 轴与 $y$- 轴的并集.

几何视角	代数视角
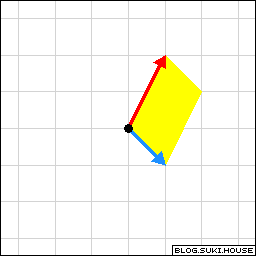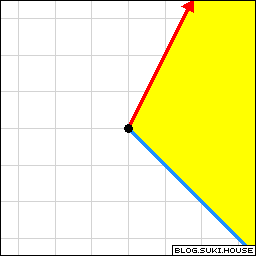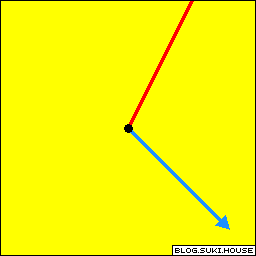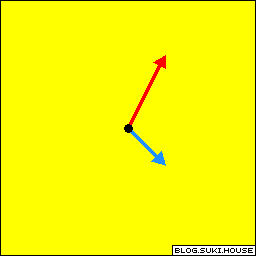
图1.4.1: 两个向量张成了全平面	$\operatorname{\mathrm{span}} A=$ 全平面 $\operatorname{\mathrm{rank}} A=2$

定义 1.4.3 向量组 $A$ 张成的空间的维数称作向量组的秩, 记作 $\operatorname{\mathrm{rank}} A$. 即

$$\operatorname{\mathrm{rank}} A=\dim \operatorname{\mathrm{span}} A$$

其中 $\dim \operatorname{\mathrm{span}} A$ 是指空间 $\operatorname{\mathrm{span}} A$ 的维数.

例 1.4.4 图 1.4.1 中的向量组秩为 2, 图 1.3.1 中的向量组秩为 1, 图 1.3.2 中的向量组秩为 2, 图 1.3.3 中的向量组秩为 3.

定义 1.4.5 向量组 $A$ 的一个 $r$ 阶子向量组是指从 $A$ 中取 $r$ 个向量构成的新向量组.

  图 1.3.2 中, $\operatorname{\mathrm{span}}(\color{red}{\boldsymbol a}, \color{blue}{\boldsymbol b}, \color{green}{\boldsymbol c})$ 和 $\operatorname{\mathrm{span}}(\color{red}{\boldsymbol a}, \color{blue}{\boldsymbol b})$ 是完全一样的. 用这两个向量完全可以描述向量组的张成空间, 而剩余的一个向量不是必须的. 也就是说向量组 $(\color{red}{\boldsymbol a}, \color{blue}{\boldsymbol b})$ 和 $A=(\color{red}{\boldsymbol a}, \color{blue}{\boldsymbol b}, \color{green}{\boldsymbol c})$ 是"等效"的. 其实这是因为 $\color{green}{\boldsymbol c}$ 是 $(\color{red}{\boldsymbol a}, \color{blue}{\boldsymbol b})$ 的线性组合, 所以 $\color{green}{\boldsymbol c}$ 必在 $(\color{red}{\boldsymbol a}, \color{blue}{\boldsymbol b})$ 张成的平面上, 所以 $\color{green}{\boldsymbol c}$ 当然是非必须的.

  另外, 可以验证, 在 $A$ 的所有子向量组中, $(\color{red}{\boldsymbol a}, \color{blue}{\boldsymbol b})$ 是向量数量最少的, 只有 2 个. 就是说 $A$ 没有由 1 个向量构成的"等效子向量组".

  根据上面的分析, 要求一个向量组的"向量个数最少的等效向量组", 只要不停地从向量组中筛掉与其余向量线性相关的向量. 每次筛除一个, 直到不能筛为止. 剩下的向量构成的向量组应该是线性无关的. 它就是所求的"向量个数最少的等效向量组".

  下面给出前述"向量个数最少的等效向量组"的严格定义.

定义 1.4.6 向量组 $B$ 是向量组 $A$ 的一个极大无关组 (等价于是上面说的"向量个数最少的等效向量组"), 如果

• $B$ 是一个线性无关的 $r$ 阶子向量组;
• $A$ 的任意一个 $r+1$ 阶子向量组都是线性相关的.

例 1.4.7 图 1.3.2 中的向量组 $(\color{red}{\boldsymbol a}, \color{blue}{\boldsymbol b}, \color{green}{\boldsymbol c})$ 有 3 个极大无关组, 即 $(\color{red}{\boldsymbol a}, \color{blue}{\boldsymbol b}),\ (\color{red}{\boldsymbol a}, \color{green}{\boldsymbol c}),\ (\color{blue}{\boldsymbol b}, \color{green}{\boldsymbol c})$. 每一个极大无关组中都有 2 个向量.

  上述定义 1.4.3 中关于维数的定义是模糊的. 现利用极大无关组的理论, 给出秩的准确定义.

定义 1.4.8 向量组 $A$ 的秩是 $A$ 的极大无关组中的向量个数.

---

附录 1.A 正文中定理的证明

定理 1.3.6 的证明

  先证必要性. 已知 $A=(\boldsymbol a_1,\boldsymbol a_2,\cdots,\boldsymbol a_n)$ 线性相关. 不妨设 $\boldsymbol a_n$ 能被其余向量线性表出.

$\Longrightarrow \exists k_1,k_2,\cdots,k_{n-1}$ 使得 $\boldsymbol a_n=k_1\boldsymbol a_1+k_2\boldsymbol a_2+\cdots+k_{n-1}\boldsymbol a_{n-1}$

$\Longrightarrow \boldsymbol 0=k_1\boldsymbol a_1+k_2\boldsymbol a_2+\cdots+k_{n-1}\boldsymbol a_{n-1}-\boldsymbol a_n$ 有非零解 $(k_1,k_2,\cdots,k_{n-1},-1)$

  再证充分性. 已知方程 $k_1\boldsymbol a_1+k_2\boldsymbol a_2+\cdots+k_n\boldsymbol a_n=\boldsymbol 0$ 有非零解. 不妨设 $k_n\neq 0$.

$\Longrightarrow \frac{k_1}{k_n}\boldsymbol a_1+\frac{k_2}{k_n}\boldsymbol a_2+\cdots+\frac{k_{n-1}}{k_n}\boldsymbol a_{n-1}-\boldsymbol a_n=\boldsymbol 0$

$\Longrightarrow \frac{k_1}{k_n}\boldsymbol a_1+\frac{k_2}{k_n}\boldsymbol a_2+\cdots+\frac{k_{n-1}}{k_n}\boldsymbol a_{n-1}=\boldsymbol a_n$, 即 $\boldsymbol a_n$ 能被其余向量线性表出. ■