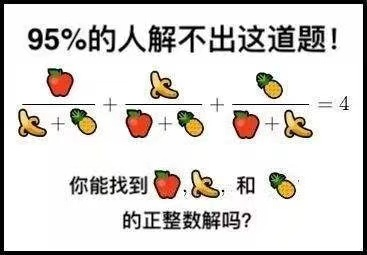
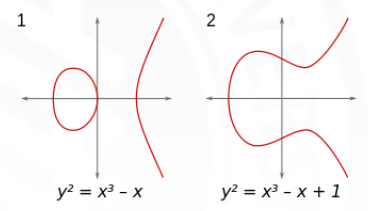方程 a b + c + b a + c + c a + b = 4 \frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}=4 b + c a + a + c b + a + b c = 4
摘 要 本文旨在阐述以下数学问题的解答过程.
这是一道“钓鱼题”: 题面十分简单, 但解答它需要使用复杂的数学知识. 在网络上, 它被称为“史上最贱的数学题”. 2014 年, Andrew Bremnera 和 Allan Macleod[1] 研究了这一系列方程的解法; 2017 年, Alon Amit[2] 具体计算了该问题的解并发布在 Quora 上. 该问题的最小正整数解在 1 0 80 10^{80} 1 0 80
本题的最小正整数解为
a = 154476802108746166441951315019919837485664325669565431700026634898253202035277999 b = 36875131794129999827197811565225474825492979968971970996283137471637224634055579 c = 4373612677928697257861252602371390152816537558161613618621437993378423467772036 本文现阐述导出该答案的步骤.
1 方程的化简
我们要求解的方程为
a b + c + b a + c + c a + b = k , a , b , c , k ∈ N + \frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}=k,\quad a,b,c,k\in\mathbb N_+ b + c a + a + c b + a + b c = k , a , b , c , k ∈ N + 对其通分, 它等价于
a ( a + b ) ( a + c ) + b ( a + b ) ( b + c ) + c ( a + c ) ( b + c ) = k ( a + b ) ( a + c ) ( b + c ) a(a+b)(a+c)+b(a+b)(b+c)+c(a+c)(b+c)=k(a+b)(a+c)(b+c) a ( a + b ) ( a + c ) + b ( a + b ) ( b + c ) + c ( a + c ) ( b + c ) = k ( a + b ) ( a + c ) ( b + c ) 进一步整理得
a 3 + b 3 + c 3 + ( 1 − k ) ( a 2 b + a b 2 + a 2 c + a c 2 + b 2 c + b c 2 ) + ( 3 − 2 k ) a b c = 0 a^3+b^3+c^3+(1-k)(a^2b+ab^2+a^2c+ac^2+b^2c+bc^2)+(3-2k)abc=0 a 3 + b 3 + c 3 + ( 1 − k ) ( a 2 b + a b 2 + a 2 c + a c 2 + b 2 c + b c 2 ) + ( 3 − 2 k ) ab c = 0 解析几何和代数知识告诉我们, 这是一条齐次方程, 它可以通过两边同除 a 3 a^3 a 3
x y 2 + E y = A x 3 + B x 2 + C x + D xy^2+Ey=Ax^3+Bx^2+Cx+D x y 2 + E y = A x 3 + B x 2 + C x + D 这样的三次曲线研究起来是复杂的, 故本题暂不这样做.
1.1 线性变换
观察原方程化简前的结构, 先作一个关于 ( a , b ) (a,b) ( a , b )
{ u = ( a + c ) + ( b + c ) = a + b + 2 c v = ( a + c ) − ( b + c ) = a − b ⟺ { a = ( u + v ) / 2 − c b = ( u − v ) / 2 − c \left\{\begin{aligned}&u=(a+c)+(b+c)=a+b+2c\\&v=(a+c)-(b+c)=a-b\end{aligned}\right. \iff \left\{\begin{aligned}&a=(u+v)/2-c\\&b=(u-v)/2-c\end{aligned}\right. { u = ( a + c ) + ( b + c ) = a + b + 2 c v = ( a + c ) − ( b + c ) = a − b ⟺ { a = ( u + v ) /2 − c b = ( u − v ) /2 − c 代入化简, 得到
( ( k + 2 ) u − ( 2 k + 5 ) c ) v 2 = ( k − 2 ) u 3 + ( 7 − 2 k ) c u 2 − 8 c 2 u \Big((k+2)u-(2k+5)c\Big)v^2=(k-2)u^3+(7-2k)cu^2-8c^2u ( ( k + 2 ) u − ( 2 k + 5 ) c ) v 2 = ( k − 2 ) u 3 + ( 7 − 2 k ) c u 2 − 8 c 2 u 可以立刻看到这样换元的好处: 现在 v v v v 2 v^2 v 2 w = ( k + 2 ) u − ( 2 k + 5 ) c w=(k+2)u-(2k+5)c w = ( k + 2 ) u − ( 2 k + 5 ) c
( 4 k 2 + 20 k + 25 ) v 2 w = − ( 2 k + 12 ) u 3 + ( 4 k 2 + 12 k − 3 ) u 2 w − 8 u w 2 (4k^2+20k+25)v^2w=-(2k+12)u^3+(4k^2+12k-3)u^2w-8uw^2 ( 4 k 2 + 20 k + 25 ) v 2 w = − ( 2 k + 12 ) u 3 + ( 4 k 2 + 12 k − 3 ) u 2 w − 8 u w 2 这里 u , v , w ∈ Q u,v,w\in \mathbb Q u , v , w ∈ Q u , v , w u,v,w u , v , w v v v
1.2 减少未知元
现在可以将方程两边同除 w 3 w^3 w 3
( 4 k 2 + 20 k + 25 ) ( v w ) 2 = − ( 2 k + 12 ) ( u w ) 3 + ( 4 k 2 + 12 k − 3 ) ( u w ) 2 − 8 ( v w ) (4k^2+20k+25)\left(\frac vw\right)^2=-(2k+12)\left(\frac uw\right)^3+(4k^2+12k-3)\left(\frac uw\right)^2-8\left(\frac vw\right) ( 4 k 2 + 20 k + 25 ) ( w v ) 2 = − ( 2 k + 12 ) ( w u ) 3 + ( 4 k 2 + 12 k − 3 ) ( w u ) 2 − 8 ( w v ) 这里理应作代换 x = u / w , y = v / w x=u/w,\ y=v/w x = u / w , y = v / w A , B A,B A , B x = A u / w , y = B v / w x=Au/w,y=Bv/w x = A u / w , y = B v / w
A 2 B 2 ( 2 k + 5 ) 2 y 2 = − 4 k + 12 A x 3 + ( 4 k 2 + 12 k − 3 ) x 2 − 8 A 2 B 2 x \frac{A^2}{B^2}(2k+5)^2y^2=-\frac{4k+12}{A}x^3+(4k^2+12k-3)x^2-8A^2B^2x B 2 A 2 ( 2 k + 5 ) 2 y 2 = − A 4 k + 12 x 3 + ( 4 k 2 + 12 k − 3 ) x 2 − 8 A 2 B 2 x 这里 x , y ∈ Q , A , B ∈ Z x,y\in\mathbb Q,\ A,B\in\mathbb Z x , y ∈ Q , A , B ∈ Z y 2 y^2 y 2 x 3 x^3 x 3 1 1 1
{ A 2 B 2 ( 2 k + 5 ) 2 = 1 − 4 k + 12 A = 1 ⟺ { A = − ( 4 k + 12 ) B = ± ( 8 k 2 + 44 k + 60 ) \left\{\begin{aligned}&\frac{A^2}{B^2}(2k+5)^2=1\\&-\frac{4k+12}{A}=1\end{aligned}\right. \iff \left\{\begin{aligned}&A=-(4k+12)\\&B=\pm(8k^2+44k+60)\end{aligned}\right. ⎩ ⎨ ⎧ B 2 A 2 ( 2 k + 5 ) 2 = 1 − A 4 k + 12 = 1 ⟺ { A = − ( 4 k + 12 ) B = ± ( 8 k 2 + 44 k + 60 ) 曲线方程变为
y 2 = x 3 + ( 4 k 2 + 12 k − 3 ) x 2 + ( 32 k + 96 ) x y^2=x^3+(4k^2+12k-3)x^2+(32k+96)x y 2 = x 3 + ( 4 k 2 + 12 k − 3 ) x 2 + ( 32 k + 96 ) x 综上, 我们完成了方程的化简. 从 ( a , b , c , k ) (a,b,c,k) ( a , b , c , k ) ( x , y ) (x,y) ( x , y )
{ x = − 4 ( k + 3 ) ( a + b + 2 c ) ( k + 2 ) ( a + b ) − c y = ± 4 ( k + 3 ) ( 2 k + 5 ) ( a − b ) ( k + 2 ) ( a + b ) − c ⟺ { a = C ( x ∓ y − ( 8 k + 24 ) ) b = C ( x ± y − ( 8 k + 24 ) ) c = C ( ( 2 k + 4 ) x + ( 8 k + 24 ) ) \left\{\begin{aligned}&x=\frac{-4(k+3)(a+b+2c)}{(k+2)(a+b)-c}\\&y=\frac{\pm 4(k+3)(2k+5)(a-b)}{(k+2)(a+b)-c}\end{aligned}\right. \iff \left\{\begin{aligned}&a=C\Big(x\mp y-(8k+24)\Big)\\&b=C\Big(x\pm y-(8k+24)\Big)\\&c=C\Big((2k+4)x+(8k+24)\Big)\end{aligned}\right. ⎩ ⎨ ⎧ x = ( k + 2 ) ( a + b ) − c − 4 ( k + 3 ) ( a + b + 2 c ) y = ( k + 2 ) ( a + b ) − c ± 4 ( k + 3 ) ( 2 k + 5 ) ( a − b ) ⟺ ⎩ ⎨ ⎧ a = C ( x ∓ y − ( 8 k + 24 ) ) b = C ( x ± y − ( 8 k + 24 ) ) c = C ( ( 2 k + 4 ) x + ( 8 k + 24 ) ) 其中 C C C k = 4 k=4 k = 4 B B B
{ x = − 28 ( a + b + 2 c ) 6 ( a + b ) − c y = 364 ( a − b ) 6 ( a + b ) − c ⟺ { a = C ( x − y − 56 ) b = C ( x + y − 56 ) c = C ( 12 x + 56 ) \left\{\begin{aligned}&x=\frac{-28(a+b+2c)}{6(a+b)-c}\\&y=\frac{364(a-b)}{6(a+b)-c}\end{aligned}\right. \iff \left\{\begin{aligned}&a=C(x-y-56)\\&b=C(x+y-56)\\&c=C(12x+56)\end{aligned}\right. ⎩ ⎨ ⎧ x = 6 ( a + b ) − c − 28 ( a + b + 2 c ) y = 6 ( a + b ) − c 364 ( a − b ) ⟺ ⎩ ⎨ ⎧ a = C ( x − y − 56 ) b = C ( x + y − 56 ) c = C ( 12 x + 56 ) 2 椭圆曲线有理点的加法运算
上一节中得到了一条代数曲线
y 2 = x 3 + p x 2 + q x , p = 4 k 2 + 12 k − 3 , q = 32 k + 96 y^2=x^3+px^2+qx,\quad p=4k^2+12k-3,\quad q=32k+96 y 2 = x 3 + p x 2 + q x , p = 4 k 2 + 12 k − 3 , q = 32 k + 96 这是一条椭圆曲线, 下面对椭圆曲线作简介.
2.1 椭圆曲线
椭圆曲线的一般方程为
y 2 + D x y + E y = x 3 + A x 2 + B x + C y^2+Dxy+Ey=x^3+Ax^2+Bx+C y 2 + D x y + E y = x 3 + A x 2 + B x + C 它可以化简为
y 2 = x 3 + B x + C y^2=x^3+Bx+C y 2 = x 3 + B x + C 的 Weierstrass 形式, 或者
y 2 = x 3 + A x 2 + B x + C y^2=x^3+Ax^2+Bx+C y 2 = x 3 + A x 2 + B x + C 的长 Weierstrass 形式, 并且它的特征方程
x 3 + A x 2 + B x + C = 0 x^3+Ax^2+Bx+C=0 x 3 + A x 2 + B x + C = 0 不能有重根, 即它的判别式 Δ \Delta Δ
Δ = − 4 A 3 C + A 2 B 2 + 18 A B C − 4 B 3 − 27 C 2 ≠ 0 \Delta=-4A^3C+A^2B^2+18ABC-4B^3-27C^2\neq 0 Δ = − 4 A 3 C + A 2 B 2 + 18 A BC − 4 B 3 − 27 C 2 = 0 一般来说, 椭圆曲线有两类图像. Δ > 0 \Delta>0 Δ > 0 Δ < 0 \Delta<0 Δ < 0
对于本题中的方程, 我们可以验证它是否是一条椭圆曲线. 考虑特征方程的判别式
Δ = p 2 q 2 − 4 q 3 = 1024 ( k + 3 ) 2 ( 2 k − 3 ) ( 2 k + 5 ) 3 \Delta=p^2q^2-4q^3=1024(k+3)^2(2k-3)(2k+5)^3 Δ = p 2 q 2 − 4 q 3 = 1024 ( k + 3 ) 2 ( 2 k − 3 ) ( 2 k + 5 ) 3 首先我们指出, 本题允许的 k k k
1 A + 1 B + 1 C ≥ 9 A + B + C , ∀ A , B , C ≥ 0 \frac 1A+\frac 1B+\frac 1C\geq \frac 9{A+B+C},\quad \forall A,B,C\geq 0 A 1 + B 1 + C 1 ≥ A + B + C 9 , ∀ A , B , C ≥ 0 当且仅当 A = B = C A=B=C A = B = C
k = a b + c + b a + c + c a + b = ( a + b + c ) ( 1 b + c + 1 a + c + 1 a + b ) − 3 ≥ ( a + b + c ) ⋅ 9 2 ( a + b + c ) − 3 = 1.5 \begin{aligned}k=\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}&=(a+b+c)\left(\frac{1}{b+c}+\frac{1}{a+c}+\frac{1}{a+b}\right)-3\\&\geq (a+b+c)\cdot\frac{9}{2(a+b+c)}-3=1.5\end{aligned} k = b + c a + a + c b + a + b c = ( a + b + c ) ( b + c 1 + a + c 1 + a + b 1 ) − 3 ≥ ( a + b + c ) ⋅ 2 ( a + b + c ) 9 − 3 = 1.5 当且仅当 a = b = c a=b=c a = b = c
a = b = c a=b=c a = b = c k k k 1.5 1.5 1.5 a = b = c a=b=c a = b = c a , b , c a,b,c a , b , c k > 1.5 k>1.5 k > 1.5 Δ > 0 \Delta>0 Δ > 0
2.2 椭圆曲线有理点及其加法
现定义椭圆曲线上有理点的加法: 给定两个曲线上的有理点 P 1 ( x 1 , y 1 ) , P 2 ( x 2 , y 2 ) P_1(x_1,y_1),P_2(x_2,y_2) P 1 ( x 1 , y 1 ) , P 2 ( x 2 , y 2 ) x 1 , y 1 , x 2 , y 2 ∈ Q x_1,y_1,x_2,y_2\in \mathbb Q x 1 , y 1 , x 2 , y 2 ∈ Q P 1 , P 2 P_1,P_2 P 1 , P 2 P 1 + P 2 P_1+P_2 P 1 + P 2 x x x
特殊地, 当 P 1 = P 2 = P P_1=P_2=P P 1 = P 2 = P P + P P+P P + P 2 P 2P 2 P
定义点 P P P x x x − P -P − P P + ( − P ) P+(-P) P + ( − P ) O \mathcal O O P − P = O P-P=\mathcal O P − P = O
以上我们完成了椭圆曲线有理点上加法运算的构造. 它具有以下性质:
封闭性, 若 P 1 , P 2 P_1,P_2 P 1 , P 2 P 1 + P 2 P_1+P_2 P 1 + P 2
结合律, ( P 1 + P 2 ) + P 3 = P 1 + ( P 2 + P 3 ) (P_1+P_2)+P_3=P_1+(P_2+P_3) ( P 1 + P 2 ) + P 3 = P 1 + ( P 2 + P 3 )
存在逆元, 即每个 P P P − P -P − P
存在单位元, 即无穷远点 O \mathcal O O P + O = O + P = P P+\mathcal O=\mathcal O+P=P P + O = O + P = P
交换律, P 1 + P 2 = P 2 + P 1 P_1+P_2=P_2+P_1 P 1 + P 2 = P 2 + P 1
其中第一条性质是重要的, 它可以通过已知的有理点构造新的有理点.
值得一提的是, 椭圆曲线作为客串角色出现在了今年 (2023 年) 2 月四省联考数学试题中, 原题如下:
22、 (12 分)
椭圆曲线加密算法运用于区块链.
椭圆曲线 C = { ( x , y ) ∣ y 2 = x 3 + a x + b , 4 a 3 + 27 b 2 ≠ 0 } C=\{(x,y)\mid y^2=x^3+ax+b,\ 4a^3+27b^2\neq 0\} C = {( x , y ) ∣ y 2 = x 3 + a x + b , 4 a 3 + 27 b 2 = 0 } P ∈ C P\in C P ∈ C x x x P ~ \tilde P P ~ C C C P ( x , y ) ( y ≠ 0 ) P(x,y)\ (y\neq 0) P ( x , y ) ( y = 0 ) y = ± x 3 + a x + b y=\pm \sqrt{x^3+ax+b} y = ± x 3 + a x + b P P P ⊕ \oplus ⊕
若 P ∈ C , Q ∈ C P\in C,\ Q\in C P ∈ C , Q ∈ C P Q PQ PQ C C C R R R P ⊕ Q = R ~ P\oplus Q=\tilde R P ⊕ Q = R ~
若 P ∈ C , Q ∈ C P\in C,\ Q\in C P ∈ C , Q ∈ C P Q PQ PQ C C C P P P P ⊕ Q = P ~ P\oplus Q=\tilde P P ⊕ Q = P ~
若 P ∈ C P\in C P ∈ C P ⊕ P ~ = 0 ∗ P\oplus \tilde P=0^* P ⊕ P ~ = 0 ∗ P ⊕ 0 ∗ = 0 ∗ ⊕ P = P P\oplus 0^*=0^*\oplus P=P P ⊕ 0 ∗ = 0 ∗ ⊕ P = P
(1) 当 4 a 3 + 27 b 2 = 0 4a^3+27b^2=0 4 a 3 + 27 b 2 = 0 h ( x ) = x 3 + a x + b h(x)=x^3+ax+b h ( x ) = x 3 + a x + b
(2) 已知“⊕ \oplus ⊕ P ∈ C , Q ∈ C P\in C,\ Q\in C P ∈ C , Q ∈ C P Q PQ PQ C C C P P P P ⊕ P = Q ~ P\oplus P=\tilde Q P ⊕ P = Q ~
(3) 已知 P ( x 1 , y 1 ) ∈ C , Q ( x 2 , y 2 ) ∈ C P(x_1,y_1)\in C,\ Q(x_2,y_2)\in C P ( x 1 , y 1 ) ∈ C , Q ( x 2 , y 2 ) ∈ C P Q PQ PQ C C C P ⊕ Q P\oplus Q P ⊕ Q
参考公式: m 3 − n 3 = ( m − n ) ( m 2 + m n + n 2 ) m^3-n^3=(m-n)(m^2+mn+n^2) m 3 − n 3 = ( m − n ) ( m 2 + mn + n 2 )
该题构造的 ⊕ \oplus ⊕ P ~ \tilde P P ~ 0 ∗ 0^* 0 ∗ − P -P − P O \mathcal O O
3 正整数解的导出
铺垫已经结束, 现在我们对摘要中的问题进行求解, 即求
a b + c + b a + c + c a + b = 4 \frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}=4 b + c a + a + c b + a + b c = 4 的正整数解.
3.1 求正整数解的步骤
现在的思路已经明确: 那就是找到椭圆曲线
y 2 = x 3 + p x 2 + q x , p = 4 k 2 + 12 k − 3 , q = 32 k + 96 y^2=x^3+px^2+qx,\quad p=4k^2+12k-3,\quad q=32k+96 y 2 = x 3 + p x 2 + q x , p = 4 k 2 + 12 k − 3 , q = 32 k + 96 的有理点 P P P ( a , b , c ) (a,b,c) ( a , b , c )
{ a = t ( x ∓ y − ( 8 k + 24 ) ) b = t ( x ± y − ( 8 k + 24 ) ) c = t ( ( 2 k + 4 ) x + ( 8 k + 24 ) ) \left\{\begin{aligned}&a=t\Big(x\mp y-(8k+24)\Big)\\&b=t\Big(x\pm y-(8k+24)\Big)\\&c=t\Big((2k+4)x+(8k+24)\Big)\end{aligned}\right. ⎩ ⎨ ⎧ a = t ( x ∓ y − ( 8 k + 24 ) ) b = t ( x ± y − ( 8 k + 24 ) ) c = t ( ( 2 k + 4 ) x + ( 8 k + 24 ) ) 因为代换式括号内均为有理数, 所以 t t t ( a , b , c ) (a,b,c) ( a , b , c ) t t t a > 0 a>0 a > 0
然后验证 ( a , b , c ) (a,b,c) ( a , b , c ) P P P 2 P 2P 2 P ( a , b , c ) (a,b,c) ( a , b , c ) n P nP n P ( a , b , c ) (a,b,c) ( a , b , c )
通过计算可以得出, 若椭圆曲线上有点 P 1 ( x 1 , y 1 ) , P 2 ( x 2 , y 2 ) P_1(x_1,y_1),\ P_2(x_2,y_2) P 1 ( x 1 , y 1 ) , P 2 ( x 2 , y 2 ) ( P 1 + P 2 ) (P_1+P_2) ( P 1 + P 2 )
{ x = λ 2 − p − x 1 − x 2 y = − ( λ ( x − x 1 ) + y 1 ) , λ = { y 2 − y 1 x 2 − x 1 , P 1 ≠ P 2 3 x 1 2 + 2 m x 1 + n 2 y 1 , P 1 = P 2 \left\{\begin{aligned}&x=\lambda^2-p-x_1-x_2\\&y=-\Big(\lambda(x-x_1)+y_1\Big)\end{aligned}\right.,\qquad \lambda=\left\{\begin{aligned}&\frac{y_2-y_1}{x_2-x_1},\ &&P_1\neq P_2\\&\frac{3x_1^2+2mx_1+n}{2y_1},\ &&P_1=P_2\end{aligned}\right. ⎩ ⎨ ⎧ x = λ 2 − p − x 1 − x 2 y = − ( λ ( x − x 1 ) + y 1 ) , λ = ⎩ ⎨ ⎧ x 2 − x 1 y 2 − y 1 , 2 y 1 3 x 1 2 + 2 m x 1 + n , P 1 = P 2 P 1 = P 2 3.2 k = 4 k=4 k = 4
现在我们可以解答摘要中的问�题了. 取 k = 4 k=4 k = 4 a a a k = t 2 + t + 4 k=t^2+t+4 k = t 2 + t + 4 x = − 4 ( t 2 + t + 1 ) 2 x=-4(t^2+t+1)^2 x = − 4 ( t 2 + t + 1 ) 2
P ( − 4 ( t 2 + t + 1 ) 2 , ± 4 ( 2 t + 1 ) ( t 2 + t + 1 ) ( 3 t 2 + 3 t + 7 ) ) P\Big(-4(t^2+t+1)^2,\pm 4(2t+1)(t^2+t+1)(3t^2+3t+7)\Big) P ( − 4 ( t 2 + t + 1 ) 2 , ± 4 ( 2 t + 1 ) ( t 2 + t + 1 ) ( 3 t 2 + 3 t + 7 ) ) 在本题中, 我们由 k = 4 k=4 k = 4 t = 0 t=0 t = 0 P ( − 4 , 28 ) P(-4,28) P ( − 4 , 28 ) ( a , b , c ) (a,b,c) ( a , b , c )
P ( − 4 , 28 ) , ( a , b , c ) = ( 11 , 4 , − 1 ) P(-4,28),\quad (a,b,c)=(11, 4, -1) P ( − 4 , 28 ) , ( a , b , c ) = ( 11 , 4 , − 1 ) 其中 c < 0 c<0 c < 0 ( P 1 + P 2 ) (P_1+P_2) ( P 1 + P 2 ) P + P = 2 P P+P=2P P + P = 2 P ( a , b , c ) (a,b,c) ( a , b , c )
2 P ( 676 49 , 55796 343 ) , ( a , b , c ) = ( 8784 , − 5165 , − 9499 ) 2P\left(\frac{676}{49},\frac{55796}{343}\right),\quad (a,b,c)=(8784,-5165,-9499) 2 P ( 49 676 , 343 55796 ) , ( a , b , c ) = ( 8784 , − 5165 , − 9499 ) 仍不符合要求. 计算 2 P + P = 3 P 2P+P=3P 2 P + P = 3 P ( a , b , c ) (a,b,c) ( a , b , c )
3 P ( − 731025 11881 , 527529870 1295029 ) , ( a , b , c ) = ( 679733219 , − 375326521 , 883659076 ) 3P\left(-\frac{731025}{11881},\frac{527529870}{1295029}\right),\quad (a,b,c)=(679733219, -375326521, 883659076) 3 P ( − 11881 731025 , 1295029 527529870 ) , ( a , b , c ) = ( 679733219 , − 375326521 , 883659076 ) 这一组解已经很大了, 但是仍不满足要求. 事实上, 我们需要持续计算到 9 P 9P 9 P ( a , b , c ) (a,b,c) ( a , b , c )
x = -66202368404229585264842409883878874707453676645038225 / 13514400292716288512070907945002943352692578000406921 y = 58800835157308083307376751727347181330085672850296730351871748713307988700611210 / 1571068668597978434556364707291896268838086945430031322196754390420280407346469 a = 154476802108746166441951315019919837485664325669565431700026634898253202035277999 b = 36875131794129999827197811565225474825492979968971970996283137471637224634055579 c = 4373612677928697257861252602371390152816537558161613618621437993378423467772036 这一组 ( a , b , c ) (a,b,c) ( a , b , c ) ( 81 , 80 , 79 ) (81,80,79) ( 81 , 80 , 79 )
4 椭圆曲线上的所有有理点
Andrew Bremnera 和 Allan Macleod[1] 的文章包含了对该问题的更多讨论. 在剩余章节中, 本文阐述一些该文章的其他结论. 首先是关于椭圆曲线
y 2 = x 3 + p x 2 + q x y^2=x^3+px^2+qx y 2 = x 3 + p x 2 + q x 上所有有理点的结构.
4.1 周期�部分
在上一小节中, 我们通过找到了一个起始有理点 P P P P P P n n n n P = O nP=\mathcal O n P = O P , 2 P , … , ( n − 1 ) P P,2P,\dots,(n-1)P P , 2 P , … , ( n − 1 ) P ( a , b , c ) (a,b,c) ( a , b , c )
n P = O , ( n + 1 ) P = P , ( n + 2 ) P = 2 P , … nP=\mathcal O,\quad (n+1)P=P,\quad (n+2)P=2P,\quad \dots n P = O , ( n + 1 ) P = P , ( n + 2 ) P = 2 P , … 都不会是解. 换言之, 通过这一个初始有理点 P P P P P P n P = O nP=\mathcal O n P = O n n n P P P o r d P \mathop{\rm ord}P ord P
实际上, 不考虑 k = 2 k=2 k = 2 n P = O nP=\mathcal O n P = O 6 6 6
4.1.1 阶为 2 2 2
第一类是使 2 P = O 2P=\mathcal O 2 P = O P = − P P=-P P = − P 1 1 1 x x x
x 3 + p x 2 + q x = 0 ⟺ x ( x − α ) ( x − β ) = 0 x^3+px^2+qx=0\iff x(x-\alpha)(x-\beta)=0 x 3 + p x 2 + q x = 0 ⟺ x ( x − α ) ( x − β ) = 0 其中
{ α = 1 2 ( − p − ( 2 k + 5 ) ( 2 k + 1 ) 2 − 4 2 ) β = 1 2 ( − p + ( 2 k + 5 ) ( 2 k + 1 ) 2 − 4 2 ) \left\{\begin{aligned}\alpha=\frac 12\left(-p-(2k+5)\sqrt{(2k+1)^2-4^2}\right)\\\beta=\frac 12\left(-p+(2k+5)\sqrt{(2k+1)^2-4^2}\right)\end{aligned}\right. ⎩ ⎨ ⎧ α = 2 1 ( − p − ( 2 k + 5 ) ( 2 k + 1 ) 2 − 4 2 ) β = 2 1 ( − p + ( 2 k + 5 ) ( 2 k + 1 ) 2 − 4 2 ) 要使 α , β ∈ Q \alpha,\beta\in\mathbb Q α , β ∈ Q ( 2 k + 1 ) 2 − 4 2 ∈ Z \sqrt{(2k+1)^2-4^2}\in\mathbb Z ( 2 k + 1 ) 2 − 4 2 ∈ Z ( 3 , 4 , 5 ) (3,4,5) ( 3 , 4 , 5 ) 4 4 4 2 k + 1 = 5 2k+1=5 2 k + 1 = 5 k = 2 k=2 k = 2
Q 2 − ( 0 , − 32 ) , Q 2 + ( 0 , − 5 ) , Q 2 ( 0 , 0 ) Q_2^-(0,-32),\qquad Q_2^+(0,-5),\qquad Q_2(0,0) Q 2 − ( 0 , − 32 ) , Q 2 + ( 0 , − 5 ) , Q 2 ( 0 , 0 ) k k k Q 2 ( 0 , 0 ) Q_2(0,0) Q 2 ( 0 , 0 )
4.1.2 阶为 3 3 3
第二类是使 3 P = O 3P=\mathcal O 3 P = O 2 P = − P 2P=-P 2 P = − P 2 2 2 x x x
( x − 4 ) ( 3 x 3 + 16 k ( k + 3 ) x 2 + 64 ( k + 3 ) 2 x + 256 ( k + 3 ) 2 ) = 0 (x-4)\Big(3x^3+16k(k+3)x^2+64(k+3)^2x+256(k+3)^2\Big)=0 ( x − 4 ) ( 3 x 3 + 16 k ( k + 3 ) x 2 + 64 ( k + 3 ) 2 x + 256 ( k + 3 ) 2 ) = 0 它至少有一个有理根 x = 4 x=4 x = 4
Q 3 ( 4 , 8 k + 20 ) , − Q 3 ( 4 , − 8 k − 20 ) Q_3(4,8k+20),\quad -Q_3(4,-8k-20) Q 3 ( 4 , 8 k + 20 ) , − Q 3 ( 4 , − 8 k − 20 ) 事实上, 虽然后一个因式必有三个实根, 但它们不会是有理根. 即是说这类有理点仅有这两个.
4.1.3 阶为 6 6 6
最后一类是使 6 P = O 6P=\mathcal O 6 P = O 2 P ≠ O , 3 P ≠ O 2P\neq \mathcal O,\ 3P\neq \mathcal O 2 P = O , 3 P = O 2 2 2 P 1 , P 2 P_1,P_2 P 1 , P 2 2 P 1 = 3 P 2 = O 2P_1=3P_2=\mathcal O 2 P 1 = 3 P 2 = O P = P 1 + P 2 P=P_1+P_2 P = P 1 + P 2 6 P = O 6P=\mathcal O 6 P = O
6 P = 6 ( P 1 + P 2 ) = 6 P 1 + 6 P 2 = 3 ⋅ 2 P 1 + 2 ⋅ 3 P 2 = 3 O + 2 O = O 6P=6(P_1+P_2)=6P_1+6P_2=3\cdot 2P_1+2\cdot 3P_2=3\mathcal O+2\mathcal O=\mathcal O 6 P = 6 ( P 1 + P 2 ) = 6 P 1 + 6 P 2 = 3 ⋅ 2 P 1 + 2 ⋅ 3 P 2 = 3 O + 2 O = O 例如, 取 Q 2 ( 0 , 0 ) Q_2(0,0) Q 2 ( 0 , 0 ) Q 3 ( 4 , 8 k + 20 ) Q_3(4,8k+20) Q 3 ( 4 , 8 k + 20 )
Q 2 + Q 3 = Q 6 ( 8 k + 24 , ( 8 k + 24 ) ( 2 k + 5 ) ) Q_2+Q_3=Q_6\Big(8k+24,(8k+24)(2k+5)\Big) Q 2 + Q 3 = Q 6 ( 8 k + 24 , ( 8 k + 24 ) ( 2 k + 5 ) ) 事实上, k ≠ 2 k\neq 2 k = 2 Q 2 Q_2 Q 2 Q 3 Q_3 Q 3 ± Q 6 \pm Q_6 ± Q 6
4.1.4 小结
综合来说, 如果我们承认无穷远点 O \mathcal O O k ≠ 2 k\neq 2 k = 2 O , Q 2 , ± Q 3 , ± Q 6 \mathcal O,\ Q_2,\ \pm Q_3,\ \pm Q_6 O , Q 2 , ± Q 3 , ± Q 6 n Q 6 ( n = 0 , 1 , … , 5 ) nQ_6\ (n=0,1,\dots,5) n Q 6 ( n = 0 , 1 , … , 5 )
0 Q 6 = O ( ∞ , ∞ ) 0Q_6=\mathcal O(\infty,\infty) 0 Q 6 = O ( ∞ , ∞ ) 1 Q 6 = Q 6 ( 8 k + 24 , ( 8 k + 24 ) ( 2 k + 5 ) ) 1Q_6=Q_6\big(8k+24,(8k+24)(2k+5)\big) 1 Q 6 = Q 6 ( 8 k + 24 , ( 8 k + 24 ) ( 2 k + 5 ) ) 2 Q 6 = − Q 3 ( 4 , − 8 k − 20 ) 2Q_6=-Q_3(4,-8k-20) 2 Q 6 = − Q 3 ( 4 , − 8 k − 20 ) 3 Q 6 = Q 2 ( 0 , 0 ) 3Q_6=Q_2(0,0) 3 Q 6 = Q 2 ( 0 , 0 ) 4 Q 6 = Q 3 ( 4 , 8 k + 20 ) 4Q_6=Q_3(4,8k+20) 4 Q 6 = Q 3 ( 4 , 8 k + 20 ) 5 Q 6 = − Q 6 ( 8 k + 24 , − ( 8 k + 24 ) ( 2 k + 5 ) ) 5Q_6=-Q_6\big(8k+24,-(8k+24)(2k+5)\big) 5 Q 6 = − Q 6 ( 8 k + 24 , − ( 8 k + 24 ) ( 2 k + 5 ) )
k = 2 k=2 k = 2 12 12 12 n 1 Q 2 + + n 2 Q 6 ( n 1 = 0 , 1 , n 2 = 0 , 1 , … , 5 ) n_1Q_2^++n_2Q_6\ (n_1=0,1,\ n_2=0,1,\dots,5) n 1 Q 2 + + n 2 Q 6 ( n 1 = 0 , 1 , n 2 = 0 , 1 , … , 5 )
4.2 自由部分
椭圆曲线的弱 Mordell-Weil 定理指出, 椭圆曲线上的有理点是有限生成的. 即是说, 存在有限个有理点 P 1 , … , P m P_1,\dots,P_m P 1 , … , P m
应用于本题, 该定理等价于对于椭圆曲线
y 2 = x 3 + p x 2 + q x y^2=x^3+px^2+qx y 2 = x 3 + p x 2 + q x 存在唯一一组线性无关的非周期有理点 G 1 , … , G m G_1,\dots,G_m G 1 , … , G m P P P
P = Q + n 1 G 1 + n 2 G 2 + ⋯ + n m G m P=Q+n_1G_1+n_2G_2+\cdots+n_mG_m P = Q + n 1 G 1 + n 2 G 2 + ⋯ + n m G m 的形式, 其中 Q Q Q 6 6 6 12 12 12 n i ∈ Z , ∀ i n_i\in \mathbb Z,\ \forall i n i ∈ Z , ∀ i G G G
P = Q + G P=Q+G P = Q + G 其中 Q Q Q G G G
4.3 秩
以 k = 4 k=4 k = 4 G 1 ( − 4 , 28 ) G_1(-4,28) G 1 ( − 4 , 28 ) P P P
P = Q + n 1 G 1 P=Q+n_1G_1 P = Q + n 1 G 1 的形式, 其中 Q Q Q 0 Q 0Q 0 Q 5 Q 5Q 5 Q n 1 ∈ Z n_1\in \mathbb Z n 1 ∈ Z k = 4 k=4 k = 4
O \mathcal O O ± G 1 \pm G_1 ± G 1 ± 2 G 1 \pm 2G_1 ± 2 G 1 ⋯ \cdots ⋯ O \mathcal O O ( ∞ , ∞ ) (\infty,\infty) ( ∞ , ∞ ) ( − 4 , ± 28 ) (-4,\pm 28) ( − 4 , ± 28 ) ( 676 49 , ± 55796 343 ) (\frac{676}{49},\pm \frac{55796}{343}) ( 49 676 , ± 343 55796 ) ⋯ \cdots ⋯ Q + Q+ Q + ( 56 , 728 ) (56,728) ( 56 , 728 ) ( − 224 9 , ± 5824 27 ) (-\frac{224}{9},\pm \frac{5824}{27}) ( − 9 224 , ± 27 5824 ) ( 1400 2209 , ± 1415960 103823 ) (\frac{1400}{2209},\pm \frac{1415960}{103823}) ( 2209 1400 , ± 103823 1415960 ) ⋯ \cdots ⋯ 2 Q + 2Q+ 2 Q + ( 4 , − 52 ) (4,-52) ( 4 , − 52 ) ( − 9 , ∓ 78 ) (-9,\mp 78) ( − 9 , ∓ 78 ) ( 8836 25 , ∓ 950716 125 ) (\frac{8836}{25},\mp \frac{950716}{125}) ( 25 8836 , ∓ 125 950716 ) ⋯ \cdots ⋯ 3 Q + 3Q+ 3 Q + ( 0 , 0 ) (0,0) ( 0 , 0 ) ( − 56 , ∓ 392 ) (-56,\mp 392) ( − 56 , ∓ 392 ) ( 2744 169 , ∓ 420616 2197 ) (\frac{2744}{169},\mp \frac{420616}{2197}) ( 169 2744 , ∓ 2197 420616 ) ⋯ \cdots ⋯ 4 Q + 4Q+ 4 Q + ( 4 , 52 ) (4,52) ( 4 , 52 ) ( − 100 , ± 260 ) (-100,\pm 260) ( − 100 , ± 260 ) ( 121 144 , ∓ 28171 1728 ) (\frac{121}{144},\mp \frac{28171}{1728}) ( 144 121 , ∓ 1728 28171 ) ⋯ \cdots ⋯ 5 Q + 5Q+ 5 Q + ( 56 , − 728 ) (56,-728) ( 56 , − 728 ) ( − 56 25 , ∓ 728 125 ) (-\frac{56}{25},\mp \frac{728}{125}) ( − 25 56 , ∓ 125 728 ) ( 32256 121 , ± 6883968 1331 ) (\frac{32256}{121},\pm \frac{6883968}{1331}) ( 121 32256 , ± 1331 6883968 ) ⋯ \cdots ⋯
再以 k = 6 k=6 k = 6 G 1 ( − 8 , 104 ) G_1(-8,104) G 1 ( − 8 , 104 ) P P P
P = Q + n 1 G 1 P=Q+n_1G_1 P = Q + n 1 G 1 的形式.
再以 k = 8 k=8 k = 8 n Q 6 nQ_6 n Q 6
再以 k = 32 k=32 k = 32 G 1 ( − 1 , 62 ) , G 2 ( 84100 , 25107620 ) G_1(-1,62),\ G_2(84100,25107620) G 1 ( − 1 , 62 ) , G 2 ( 84100 , 25107620 ) P P P
P = Q + n 1 G 1 + n 2 G 2 P=Q+n_1G_1+n_2G_2 P = Q + n 1 G 1 + n 2 G 2 的形式.
我们发现对于不同的 k k k k = 4 k=4 k = 4 k = 6 k=6 k = 6 1 1 1 k = 8 k=8 k = 8 0 0 0 k = 34 k=34 k = 34 2 2 2
Andrew Bremnera 和 Allan Macleod[1] 统计了 k = 1 , 2 , … , 1000 k=1,2,\dots,1000 k = 1 , 2 , … , 1000 436 436 436 0 0 0 485 485 485 1 1 1 76 76 76 2 2 2 k = 34 , 94 , 98 , … k=34,94,98,\dots k = 34 , 94 , 98 , … 3 3 3 3 3 3 k = 424 , 680 , 975 k=424,680,975 k = 424 , 680 , 975
5 正整数解对应的 x x x
本节讨论的是什么样的 ( x , y ) (x,y) ( x , y ) ( a , b , c ) (a,b,c) ( a , b , c ) a a a C C C
{ a = x − y − ( 8 k + 24 ) b = x + y − ( 8 k + 24 ) c = ( 2 k + 4 ) x + ( 8 k + 24 ) \left\{\begin{aligned}&a=x-y-(8k+24)\\&b=x+y-(8k+24)\\&c=(2k+4)x+(8k+24)\end{aligned}\right. ⎩ ⎨ ⎧ a = x − y − ( 8 k + 24 ) b = x + y − ( 8 k + 24 ) c = ( 2 k + 4 ) x + ( 8 k + 24 ) 首先令 a , b a,b a , b a b > 0 ab>0 ab > 0
− ( x − 4 ) ( x − α 1 ) ( x �− β 1 ) > 0 -(x-4)(x-\alpha_1)(x-\beta_1)>0 − ( x − 4 ) ( x − α 1 ) ( x − β 1 ) > 0 其中
α 1 = − 2 ( k + 3 ) ( k + k 2 − 4 ) , β 1 = − 2 ( k + 3 ) ( k − k 2 − 4 ) \alpha_1=-2(k+3)(k+\sqrt{k^2-4}),\quad \beta_1=-2(k+3)(k-\sqrt{k^2-4}) α 1 = − 2 ( k + 3 ) ( k + k 2 − 4 ) , β 1 = − 2 ( k + 3 ) ( k − k 2 − 4 ) 通过计算可知 α 1 ≤ β 1 < 4 \alpha_1\leq \beta_1<4 α 1 ≤ β 1 < 4 k = 2 k=2 k = 2
x ∈ ( − ∞ , α 1 ) ∪ ( β 1 , 4 ) x\in (-\infty,\alpha_1)\cup (\beta_1,4) x ∈ ( − ∞ , α 1 ) ∪ ( β 1 , 4 ) 然后令 c c c a , b a,b a , b ( a + b ) c > 0 (a+b)c>0 ( a + b ) c > 0
4 ( x − 8 k − 24 ) ( ( k + 2 ) x + 4 k + 12 ) > 0 4(x-8k-24)\Big((k+2)x+4k+12\Big)>0 4 ( x − 8 k − 24 ) ( ( k + 2 ) x + 4 k + 12 ) > 0 其中
α 2 = − 4 k + 12 k + 2 , β 2 = 8 k + 24 \alpha_2=-\frac{4k+12}{k+2},\quad \beta_2=8k+24 α 2 = − k + 2 4 k + 12 , β 2 = 8 k + 24 通过计算可知 α 2 ≤ β 2 \alpha_2\leq \beta_2 α 2 ≤ β 2
x ∈ ( − ∞ , α 2 ) ∪ ( β 2 , ∞ ) x\in (-\infty,\alpha_2)\cup (\beta_2,\infty) x ∈ ( − ∞ , α 2 ) ∪ ( β 2 , ∞ ) 最后当然, x x x
x 3 + p x 2 + q x > 0 ⟺ x ( x − α ) ( x − β ) > 0 x^3+px^2+qx>0\iff x(x-\alpha)(x-\beta)>0 x 3 + p x 2 + q x > 0 ⟺ x ( x − α ) ( x �− β ) > 0 其中
{ α = 1 2 ( − p − ( 2 k + 5 ) ( 2 k + 1 ) 2 − 4 2 ) β = 1 2 ( − p + ( 2 k + 5 ) ( 2 k + 1 ) 2 − 4 2 ) \left\{\begin{aligned}\alpha=\frac 12\left(-p-(2k+5)\sqrt{(2k+1)^2-4^2}\right)\\\beta=\frac 12\left(-p+(2k+5)\sqrt{(2k+1)^2-4^2}\right)\end{aligned}\right. ⎩ ⎨ ⎧ α = 2 1 ( − p − ( 2 k + 5 ) ( 2 k + 1 ) 2 − 4 2 ) β = 2 1 ( − p + ( 2 k + 5 ) ( 2 k + 1 ) 2 − 4 2 ) 当 k > 1.5 k>1.5 k > 1.5 α < β < 0 \alpha<\beta<0 α < β < 0 x ∈ [ α , β ] ∪ [ 0 , + ∞ ) x\in [\alpha,\beta]\cup[0,+\infty) x ∈ [ α , β ] ∪ [ 0 , + ∞ )
α < α 1 < β 1 < α 2 < β < 0 < 4 < β 2 \alpha<\alpha_1<\beta_1<\alpha_2<\beta<0<4<\beta_2 α < α 1 < β 1 < α 2 < β < 0 < 4 < β 2 所以可以总结出: ( a , b , c ) (a,b,c) ( a , b , c )
x ∈ [ α , α 1 ) ∪ ( β 1 , α 2 ) x\in[\alpha,\alpha_1)\cup (\beta_1,\alpha_2) x ∈ [ α , α 1 ) ∪ ( β 1 , α 2 ) 其中
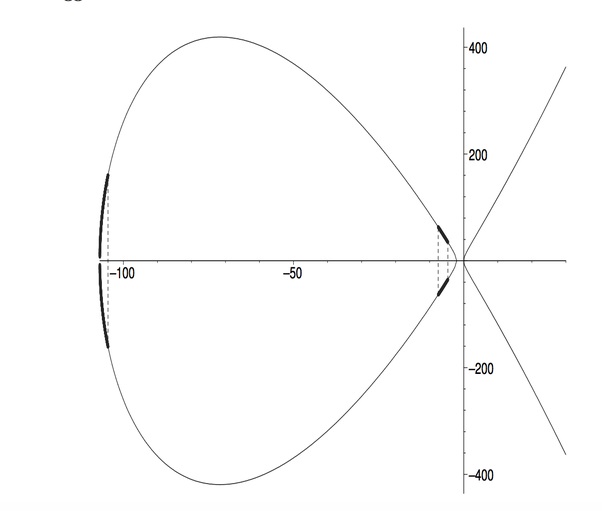
{ α = 1 2 ( − p + ( 2 k + 5 ) ( 2 k + 1 ) 2 − 4 2 ) α 1 = − 2 ( k + 3 ) ( k + k 2 − 4 ) β 1 = − 2 ( k + 3 ) ( k − k 2 − 4 ) α 2 = − 4 k + 12 k + 2 \left\{\begin{aligned}&\alpha=\frac 12\left(-p+(2k+5)\sqrt{(2k+1)^2-4^2}\right)\\&\alpha_1=-2(k+3)(k+\sqrt{k^2-4})\\&\beta_1=-2(k+3)(k-\sqrt{k^2-4})\\&\alpha_2=-\frac{4k+12}{k+2}\end{aligned}\right. ⎩ ⎨ ⎧ α = 2 1 ( − p + ( 2 k + 5 ) ( 2 k + 1 ) 2 − 4 2 ) α 1 = − 2 ( k + 3 ) ( k + k 2 − 4 ) β 1 = − 2 ( k + 3 ) ( k − k 2 − 4 ) α 2 = − k + 2 4 k + 12 这可以看出正整数解的一些特性. 从位置上说, 正整数解总在椭圆曲线的卵形线一支取到; 从区间长度上说, 可以绘制 k = 4 k=4 k = 4
即上图中粗线段对应的点是正整数解: 正整数解出现的条件是苛刻的. 计算卵形线的区间长度 β − α \beta-\alpha β − α α 1 − α \alpha_1-\alpha α 1 − α α 2 − β 1 \alpha_2-\beta_1 α 2 − β 1
k = 4 , β − α ≈ 104.81 , α 1 − α ≈ 2.41 , α 2 − β 1 ≈ 2.84 k=4,\quad \beta-\alpha\approx104.81,\quad \alpha_1-\alpha\approx 2.41,\quad \alpha_2-\beta_1\approx 2.84 k = 4 , β − α ��≈ 104.81 , α 1 − α ≈ 2.41 , α 2 − β 1 ≈ 2.84 可以看到正整数解区间只占卵形线区间的一小部分. 实际上, 当 k → ∞ k\to\infty k → ∞
β − α = O ( k 2 ) , α 1 − α → 1 , α 2 − β 1 → 0 \beta-\alpha=O(k^2),\quad \alpha_1-\alpha\to 1,\quad \alpha_2-\beta_1\to 0 β − α = O ( k 2 ) , α 1 − α → 1 , α 2 − β 1 → 0 即正整数解区间大致只占卵形线区间长度的 1 / k 2 1/k^2 1/ k 2
6 k ≤ 200 k\leq 200 k ≤ 200
Andrew Bremnera 和 Allan Macleod[1] 计算了 4 ≤ k ≤ 200 4\leq k\leq 200 4 ≤ k ≤ 200 1 1 1 k k k n n n
P = Q + n G 1 P=Q+nG_1 P = Q + n G 1 为正整数解的最小迭代次数, “位数”为 ( a , b , c ) (a,b,c) ( a , b , c )
k k k n n n 位数 k k k n n n 位数 k k k n n n 位数 4 9 81 48 311 418086 136 65 26942 6 11 134 58 221 244860 146 307 259164 10 13 190 60 61 9188 156 353 12046628 12 35 2707 66 107 215532 158 1211 15097279 14 47 1876 76 65 23662 162 457 1265063 16 11 414 82 157 85465 178 2945 398605460 18 49 10323 92 321 252817 182 853 2828781 24 107 33644 102 423 625533 184 851 20770896 28 121 81853 112 223 935970 186 643 5442988 32 65 14836 116 101 112519 196 701 11323026 38 659 1584369 126 75 196670 198 121 726373 42 419 886344 130 707 8572242 200 2957 71225279 46 201 198771 132 461 3607937
例如 k = 178 k=178 k = 178 3000 3000 3000 4 4 4 k = 896 k=896 k = 896 161477 161477 161477 2 2 2
7 总结与讨论
本文本质上是用初等方法对 Andrew Bremnera 和 Allan Macleod[1] 的工作进行了部分复现, 其中穿插了本文作者的一些补充: 例如由 ( x , y ) (x,y) ( x , y ) ( a , b , c ) (a,b,c) ( a , b , c )
除此之外, 本文还有一些遗留的问题, 例如:
寻找 k = 4 k=4 k = 4 k = t 2 + t + 4 k=t^2+t+4 k = t 2 + t + 4 k = 4 k=4 k = 4 G 1 ( − 4 , 28 ) G_1(-4,28) G 1 ( − 4 , 28 ) k = 6 k=6 k = 6 t = 1 t=1 t = 1 P ( − 36 , 468 ) = 3 Q 6 + G 1 P(-36,468)=3Q_6+G_1 P ( − 36 , 468 ) = 3 Q 6 + G 1 k k k
通过枚举 P = Q + G P=Q+G P = Q + G
这些都是本文未解决的问题.
参考文献
[1] Bremner A, Macleod A. An unusual cubic representation problem[C]//Annales Mathematicae et Informaticae. 2014: 29-41.
[2] https://www.quora.com/How-do-you-find-the-positive-integer-solutions-to-frac-x-y+z-+-frac-y-z+x-+-frac-z-x+y-4/answer/Alon-Amit