《机器学习》笔记（第一部分：绪论、模型评估与选择、线性模型）

1 绪论

1.2 基本术语

数据集 $D = \{\boldsymbol x_i\}_{i=1}^m$ 是一个包含 $m$ 个示例 (instance) 或样本 (sample) 的数据集 (data set). 每个示例用 $d$ 个属性 (attribute) 或特征 (feature) 描述, 属性张成的空间 $\mathcal X$ 称为属性空间 (attribute space) 或样本空间 (sample space) 或输入空间 (input space). 每个示例 $\boldsymbol x_i = (x_{ij})_{j=1}^d$ 是 $d$ 维样本空间 $\mathcal X = \prod _i \mathcal X_i$ 中的一个向量, 称为特征向量^注 (feature vector), 其中 $x_{ij}$ 是 $\boldsymbol x_i$ 在第 $j$ 个属性上的取值, 称为属性值 (attribute value). $d$ 称为样本 $\boldsymbol x_i$ 的维数 (dimensionality).

注 此处的“特征向量”(feature vector) 需要与线性代数中的“特征向量”(eigenvector) 区分.

训 练 从数据中学得模型的过程称为学习 (learning) 或训练 (training). 训练使用的数据称为训练数据 (training data), 单条训练数据称为训练样本 (training sample), 所有训练样本构成训练集 (training set). 训练样本的期待输出称为标记或标签 (label), 拥有标记的示例称为样例 (example). 设 $\mathcal Y$ 是所有标记的集合, 称为标记空间 (label space) 或输出空间 (output space). 一般用 $(x_i, y_i)$ 表示第 $i$ 个样例, 其中 $y_i \in \mathcal Y$ 是标记. 若标记空间 $\mathcal Y$ 是离散的 (亦即 $|\mathcal Y| \leq \aleph _0$) 则称此类学习任务是分类 (classification); 若是连续的 (亦即 $|\mathcal Y| \geq \aleph _1$), 则称是回归 (regression). 二者都是预测 (prediction) 问题, 是希望通过对训练集 $\{(\boldsymbol x_i, y_i)\}_{i=1}^m$ 学习, 建立一个预测映射 $f:X\to Y$.

分类问题 $|\mathcal Y| = 2$ 时称为二分类 (binary classification) 问题, 两类分别为正类 (positive class) 和反类 (negative class). 涉及多个类别时称为多分类 (multi-class classification) 问题. 对二分类任务, 通常令 $\mathcal Y = \mathbb B = \{+1, -1\}$ 或 $\{0, 1\}$.

测 试 学得模型后使用其进行预测的过程叫测试 (testing). 被预测的样本称为测试样本 (testing sample). 学得 $f$ 后对测试例 $\boldsymbol x^*$ 可以得到其预测标记 $y^* = f(\boldsymbol x^*)$.

无监督学习 分类和回归的训练数据都有标记信息, 属于监督学习 (supervised learning). 聚类 (clustering) 是将训练集中样本分为若干个簇 (cluster) 的算法, 属于无监督学习 (unsupervised learning).

1.3 假设空间

  学得的模型对应了关于数据的某种存在规律, 所以模型亦称假设 (hypothesis), 这种潜在规律称为真实 (ground-truth). 我们的目的是寻找与训练集匹配 (fit) 的假设. 所有假设构成的空间 $\mathcal H$ 称为假设空间 (hypothesis space), 假设空间里那些与训练集一致的假设的集合称为版本空间 (version space). 一种算法 $\mathfrak L$ 在一个训练集 $X$ 下会产生一个假设 $h$.

1.4 归纳偏好

  版本空间的所有假设在面对测试数据中会各有偏好, 称为归纳偏好 (inductive bias).

  设样本空间 $\mathcal X$ 和假设空间 $\mathcal H$ 都是离散的. 令 $\Pr(h \mid X, \mathfrak L _a)$ 是算法 $\mathfrak L _a$ 在训练集 $X$ 下产生假设 $h$ 的概率. 给定训练集 $X$, 假想存在真实目标函数 $f$ (即 $\boldsymbol x$ 与 $y$ 的真实对应关系), 定义算法 $\mathfrak L$ 对于某个样本 $\boldsymbol x^*$ 的平均误差为

$$E(\mathfrak L, \boldsymbol x^* \mid X, f) = \sum _h \bigg( \Pr(h \mid X, \mathfrak L _a) \cdot \ell(h(\boldsymbol x^*), f(\boldsymbol x^*)) \bigg)$$

其中 $\ell(\cdot, \cdot)$ 是距离函数.

  给定训练集 $X$, 假想存在真实目标函数 $f$, 定义算法 $\mathfrak L$ 的训练集外误差 (out-of-training-set error) $E _{\rm OTE}$ 是所有样本 (训练集除外) 的误差之和

$$E _{\rm OTE}(\mathfrak L \mid X, f) = \sum _{\boldsymbol x \in \mathcal X \setminus X} \bigg( \Pr(\boldsymbol x) \cdot E(\mathfrak L, \boldsymbol x \mid X, f) \bigg)$$

  现在考虑所有可能的真实目标函数 $f$ 的误差总和

$$\mathcal E = \sum _f \bigg( \Pr(f) \cdot E _{\rm OTE}(\mathfrak L \mid X, f) \bigg)$$

没有免费的午餐定理 (NFL 定理, no free lunch theorem) 假设真实目标函数 $f$ 是均匀分布的. 以二分类问题为例, $f$ 可以取遍 $\mathcal X \to \mathbb B$ 这 $2^{|\mathcal X|}$ 个函数. 将误差总和全部展开重组得到

$$\mathcal E = \sum _{\boldsymbol x \in \mathcal X \setminus X} \Bigg( \Pr(\boldsymbol x) \cdot \sum _h \bigg( \Pr(h \mid X, \mathfrak L _a) \cdot \sum _f \Big( \Pr(f) \cdot \ell(h(\boldsymbol x), f(\boldsymbol x)) \Big) \bigg) \Bigg)$$

以 $\ell(y_1, y_2) = \mathit 1_{y_1 \neq y_2}$ 为例, 此时 $\Pr(f) = 1/2^{|\mathcal x|}$, 且有恰好一半的 $f$ 能使 $f(\boldsymbol x)=0$ 或 $f(\boldsymbol x)=1$. 所以

$$\begin{aligned} \mathcal E &= \sum _{\boldsymbol x \in \mathcal X \setminus X} \Bigg( \Pr(\boldsymbol x) \cdot \sum _h \bigg( \Pr(h \mid X, \mathfrak L _a) \cdot \frac{1}{2^{|\mathcal X|}} \cdot \frac 12 \cdot 2^{|\mathcal X|} \bigg) \Bigg)\\ &= \frac 12 \sum _{\boldsymbol x \in \mathcal X \setminus X} \bigg( \Pr(\boldsymbol x) \cdot \sum _h \Big( \Pr(h \mid X, \mathfrak L _a) \Big) \bigg)\\ &= \frac 12 \sum _{\boldsymbol x \in \mathcal X \setminus X} \Big( \Pr(\boldsymbol x) \cdot 1 \Big) = \frac{1 - \Pr(X)}{2} \end{aligned}$$

以上计算的结论是: 如果真实的目标函数 $f$ 是均匀分布的, 那么预测总误差的期望 $\mathcal E$ 与具体算法 $\mathfrak L$ 无关, 聪明的学习算法在预测期望上与随机乱猜相同. 这是因为“$f$ 均匀分布”这个假设不合理, 每一个现实问题中的 $f$ 各有各的不均匀性. NFL 定理启发我们谈论算法的优劣必须要针对具体的学习问题, 学习算法的优劣与算法本身无关, 而与具体的学习问题强相关.

2 模型评估与选择

2.2 评估方法

  首先需要将数据集 $D = \{(\boldsymbol x_i, y_i)\}_{i=1}^m$ 分割为训练集 $S$ 和测试集 $T$.

留出法 (hold-out) 即把 $D = S \cup T$ 分割为两个互斥的集合, $S \cap T = \varnothing$. 训练集一般占总量的 $66\%$ 至 $80\%$. 经常使用分层采样 (stratified sampling), 即 $S$ 和 $T$ 中正反例的比例相等. 留出法一般需要使用不同的分割方法重复验证, 然后取平均误差.

交叉验证法 (cross validation) 将 $D = \bigcup _{i=1}^k D_i$ 划分为 $k$ 个大小相似的互斥子集, $\forall i, j, D_i \cap D_j = \varnothing$. 然后每次用 $D_i$ 作为测试集, 其余的子集作为训练集. 又称 $k$-倍交叉验证 ($k$-fold cross validation). 极端情况下令 $k=m$, 则 $\forall i, |D_i| = 1$, 此时成为留一法 (LOO, leave-one-out).

自助法 (bootstrapping) 即在数据集 $D$ 中重复有放回采样 $m$ 次构成测试集 $S$. 当 $m$ 很大时, 某个样本始终不被采集到的概率是

$$\lim _{m \to \infty} \left(1 - \frac 1m\right)^m = e^{-1} \approx 37\%$$

然后取测试集 $T = D \setminus S$ .这样就可以指定 $|S| = m$ 同时保证 $|T|$ 大概占总量的 $37\%$.

2.3 性能度量

查准率、查全率与 $F _\beta$ 度量 考虑分类结果的混淆矩阵 (confusion matrix)

	预测正例	预测反例
真实正例	真正例 ${\rm TP}$	假反例 ${\rm FN}$
真实反例	假正例 ${\rm FP}$	真反例 ${\rm TN}$

定义查准率 (precision) $P$ 是预测正例中真实正例的比例, 查全率 (recall) $R$ 是真实正例中预测正例的比例.

$$P = \frac{{\rm TP}}{{\rm TP} + {\rm FP}}, \quad R = \frac{{\rm TP}}{{\rm TP} + {\rm FN}}$$

定义 $F _\beta$ 度量是它们的加权调和平均值, $F _1$ 度量是 $\beta = 1$ 时的特例

$$F _\beta = \left( \frac{P ^{-1} + \beta ^2R ^{-1}}{1 + \beta ^2} \right) ^{-1}, \qquad F _1 = \left( \frac{P ^{-1} + R ^{-1}}{2} \right) ^{-1}$$

当 $\beta > 1$ 时, $F _\beta$ 更看重查全率, 适合逃犯信息系统等场合; 当 $\beta < 1$ 时更看重查准率, 适合商品精准推荐等场合. 在有多个二分类混淆矩阵时, 可以求查准率的平均值, 称为宏查准率 (macro-$P$); 也可以求平均混淆矩阵的查准率, 称为微查准率 (micro-$P$). 查全率和 $F _\beta$ 亦然.

  对于二分类问题, 一般学习到的模型 $g _\alpha \circ f$ 是两步的复合: $f: \mathcal X \to \mathbb R$ 和 $g _\alpha: \mathbb R \to \mathbb B, z \mapsto \mathit 1 _{z > \alpha}$, 其中 $\alpha$ 是一个阈值. 考虑所有这样的模型 $g _\alpha \circ f, \forall \alpha$ 的查准率与查全率, 会得到一条查准率-查全率 (P-R) 曲线 $\{(P _\alpha, R _\alpha)\} _{\forall \alpha}$, 这是一条经过 $(0, 1)$ 和 $(1, 0)$ 的上凸曲线.

ROC 曲线与 AUC 定义真正例率 (TPR, true positive rate) 和假正例率 (FPR, false positive rate) 为

$${\rm TPR} = \frac{{\rm TP}}{{\rm TP} + {\rm FN}}, \quad {\rm FPR} = \frac{{\rm FP}}{{\rm TN} + {\rm FP}}$$

考虑所有模型 $g _\alpha \circ f, \forall \alpha$ 的真正例率和假正例率, 可以得到一条假正例率-真正例率曲线, 称为受试者工作特征 (ROC, receiver operating characteristic) 曲线 $\{({\rm FPR} _\alpha, {\rm TPR} _\alpha)\} _{\forall \alpha}$, 它是一条经过 $(0, 0)$ 和 $(1, 1)$ 的上凸曲线. 定义 AUC (area under ROC curve) 为 ROC 曲线下方的面积.

  在离散情况下, 假设 $\alpha$ 有 $m$ 种取值 $\alpha _{(1)}, \dots, \alpha _{(m)}$ (排序后), $\alpha _{(i)}$ 对应 ROC 曲线上的点 $({\rm FPR} _{(i)}, {\rm TPR} _{(i)})$, 则 AUC 可以估算为

$${\rm AUC} = \sum _{i=1} ^{m-1} \frac 12({\rm FPR} _{i+1} - {\rm FPR} _i)({\rm TPR} _i + {\rm TPR} _{i+1})$$

  考虑排序误差. 令 $D^+, D^-$ 分别表示正反例集合, 定义模型 $f: \mathcal X \to \mathbb R$ 的排序损失 (rank loss) 为

$$\ell _{\rm rank} = \frac{1}{|D^+||D^-|} \sum _{\boldsymbol x^+ \in D^+} \sum _{\boldsymbol x^- \in D^-} \Bigg( \mathit 1 _{f(\boldsymbol x^+) < f(\boldsymbol x^-)} + \frac 12 \mathit 1 _{f(\boldsymbol x^+) = f(\boldsymbol x^-)} \Bigg)$$

即考虑所有正反例两两相配, 若正例预测值小于反例则记 $1$ 个罚分; 若相等则记 $1/2$ 个罚分. 排序损失对应的是 ROC 上方的面积, 即

$${\rm AUC} = 1 - \ell _{\rm rank}$$

2.4 比较检验

错误率是否等于给定值的 $t$-检验 设某个学习器的真实错误率是 $\epsilon$, 则它的观测值服从二项分布 $e \sim b(m, \epsilon)$. 若有观测值 $\{e_i\} _{i=1}^k$, 考虑这样的假设

$$H_0: e = e_0 \quad \text{v.s} \quad H_1: e \neq e_0$$

它渐进服从正态分布. 考虑它的 $t$-统计量:

$$\bar e = \frac 1k \sum _{i=1}^k e_i, \quad s ^2 = \frac{1}{k-1} \sum _{i=1}^k (e_i - \bar e) ^2, \quad t_0 = \frac{\bar e - e_0}{\sigma / \sqrt k}$$

给定置信度 $1 - \alpha$ 后可以做自由度为 $k - 1$ 的 $t$-检验, 它的拒绝域是 $\mathbb R \setminus (-t_{1-\alpha/2}, t_{1-\alpha/2})$.

两模型错误率是否相同的交叉验证 $t$-检验 若有两个学习器 A 与 B, 使用 $k$-倍交叉验证得到的错误率分别为 $\{e_i^{(A)}\} _{i=1}^k$ 和 $\{e_i^{(B)}\} _{i=1}^k$, 其中 $e_i^{(X)}$ 是第 $i$ 个测试集在学习器 X 上的错误率. 考虑 $\Delta e_i = e_i^{(A)} - e_i^{(B)}$, 它渐进服从均值为 0 的正态分布. 对其做相同的 $t$-检验

$$t_0 = \frac{\overline{\Delta e}}{\sigma_{\Delta e} / \sqrt n}$$

两模型是否协同错误的 McNemar 检验 列出两模型的正确率的列联表 (contingency table)

	算法 A 正确	算法 A 错误
算法 B 正确	$e _{00}$	$e _{01}$
算法 B 错误	$e _{10}$	$e _{11}$

McNemar 检验考虑了以下的统计量, 它是 $|e_{01} - e_{10}|$ 这个统计量在 McNemar 检验问题下的小样本修正形式

$$\chi ^2_0 = \frac{(|e_{01} - e_{10}| - 1) ^2}{e_{01} + e_{10}}$$

它服从 $\chi^2(1)$ 分布, 拒绝域是 $[\chi^2_{1-\alpha}(1), +\infty)$.

多个模型错误率是否相同的 Friedman 检验与 Nemenyi 后续检验 假设有 $k$ 个算法 $\{A_i\}_{i=1}^k$ 和 $N$ 个数据集. 在每个数据集上对各算法的性能从高到低赋予序值 $1, \dots, k$ (相同性能的取序值平均数). 计算每一个算法的平均序值 $\{r_i\}_{i=1}^k$. 首先假设所有算法性能是否都相同. 计算

$$\chi ^2_0 = \frac{12N}{k(k+1)} \sum _{i=1}^k r_i^2 - 3N(k+1)$$

是原始 Friedman 检验统计量, 当 $k$ 与 $N$ 较大时它服从 $\chi^2(k-1)$. 另外还有

$$F_0 = \frac{(N - 1)\chi^2_0}{N(k - 1) - \chi^2_0}$$

是 Friedman 检验统计量, 当 $k$ 与 $N$ 较大时它服从 $F(k-1, (k-1)(N-1))$, 拒绝域是 $[F_{1-\alpha}(k-1, (k-1)(N-1)), +\infty)$. 若假设被拒绝, 则继续考虑 Nemenyi 后续检验 (post-hoc test), 计算临界值

$${\rm CD} = q_{1-\alpha}\sqrt{\frac{k(k+1)}{6N}}$$

其中 $q_{1-\alpha}$ 是 Tukey 分布的左分位数. 若两个算法 $A_i$ 与 $A_j$ 有 $|r_i - r_j| > {\rm CD}$, 则认为这两个算法性能不相同.

2.5 偏差与方差

  总体无法被直接观测, 训练集上的预设输出也只是真实输出的观测值. 对于测试样本 $\boldsymbol x$, 令 $y$ 是它的真实标记, $y_D$ 是它在数据集中的标记, $f(\boldsymbol x, D)$ 是通过训练集 $D$ 学得模型 $f$ 在 $\boldsymbol x$ 上的预测输出.

  取遍所有可能的数据集 $D$, 可以得到一系列模型 $f(\cdot, D)$. 它们对 $\boldsymbol x$ 的预测期望是

$$\mathrm Ef(\boldsymbol x) = \mathrm E _D f(\boldsymbol x, D)$$

预测方差是

$$\mathrm Df(\boldsymbol x) = \mathrm E _D (f(\boldsymbol x, D) - Ef(\boldsymbol x)) ^2$$

期望输出与真实标记的差的平方和称为偏差平方和

$${\rm bias}^2 = (\bar f(\boldsymbol x) - y) ^2$$

样本标记与真实标记差的平方和称为噪声平方和

$$\varepsilon ^2 = \mathrm E _D(y_D - y) ^2$$

  定义泛化误差平方和是取遍所有可能的数据集 $D$ 训练得到的模型 $f_(\cdot, D)$ 的平均误差平方和, 即

$$\mathcal E(f) = \mathrm E _D(f(\boldsymbol x, D) - y_D) ^2$$

泛化误差平方和可以做如下分解

$$\mathcal E(f) = {\rm bias} ^2 + \mathrm D(f) + \varepsilon ^2$$

即泛化误差平方和可分解为偏差平方和、预测方差与噪声之和.

  偏差平方和是预测值与真实值的差值, 刻画算法的拟合能力; 预测方差是不同训练集对预测效果的扰动影响; 噪声是所有学习方法的误差下界. 一般来说偏差和方差是冲突的, 训练不足时偏差大但方差小, 训练充足后训练数据的自身轻微扰动都会发生显著变化.

3 线性模型

3.2 线性回归

线性模型 (linear model) 给定数据集 $D = \{(\boldsymbol x_i, y_i)\} _{i=1}^m$ 其中 $\boldsymbol x_i = (x_{ij}) _{j=1}^d$, $y_i \in \mathbb R$. 将数据集排成一个矩阵

$$X = \begin{pmatrix} x_{11} & \cdots & x_{1d} & 1\\ \vdots & & \vdots & \vdots\\ x_{m1} & \cdots & x_{md} & 1\\ \end{pmatrix} = \begin{pmatrix} \boldsymbol x_1^T & 1\\ \vdots & \vdots\\ \boldsymbol x_m^T & 1\\ \end{pmatrix}, \quad \boldsymbol y = \begin{pmatrix} y_1\\ \vdots\\ y_m \end{pmatrix}$$

我们试图学得一个向量 $\boldsymbol \beta \in \mathbb R ^{d+1} = (w_1, \dots, w_d, b)^T$ 使得

$$E = \sum _{i=1}^k \ell(\boldsymbol \beta^T \boldsymbol x_i, y_i) = \min$$

取 $\ell(x, y) = (x - y) ^2$, 将上式写成矩阵形式

$$E = (\boldsymbol y - X\boldsymbol \beta)^T (\boldsymbol y - X\boldsymbol \beta)$$

将其对 $\boldsymbol \beta$ 求导

$$\frac{\partial E}{\partial \boldsymbol \beta} = -2X^T(\boldsymbol y - X\boldsymbol \beta)$$

令上式等于零向量, 可以得到 $\boldsymbol \beta$ 的解析解

$$\boldsymbol \beta = (X^TX)^{-1}X^T\boldsymbol y$$

这个解析解需要 $X^TX$ 可逆.

广义线性模型 (generalized linear model) 考虑单调可导函数 $g(\cdot)$, 令模型

$$y = g^{-1}(\boldsymbol w^T \boldsymbol x + b)$$

这是广义线性模型. 其中 $g(\cdot)$ 称为联系函数 (link function).

3.3 Logistic 回归

  令 $\boldsymbol \beta = (\boldsymbol w^T, b)^T$ 以及 $\tilde{\boldsymbol x} = (\boldsymbol x, 1)$. 一般的线性回归模型 $z = \boldsymbol w^T \boldsymbol x + b = \boldsymbol \beta ^T \tilde{\boldsymbol x}$ 的值域是 $\mathbb R$. 但二分类问题希望值域是 $\mathbb B$, 所以需要一个函数 $g^{-1}(\cdot)$ 来转换. 阶跃函数 $y = \mathit 1 _{z \geq 0}$ 不连续, 此时 Logistic 函数是一个常见的替代函数

$$y = \frac{1}{1 + e^{-z}}$$

将其作为 $g^{-1}(\cdot)$, 可以得到 Logistic 回归模型

$$y = \frac{1}{1 + e^{-\boldsymbol \beta^T \tilde{\boldsymbol x}}} \iff \ln \frac{y}{1 - y} = \boldsymbol \beta^T \tilde{\boldsymbol x}$$

若将 $y$ 看作一个随机变量 $Y$, 表示样本 $\boldsymbol x$ 作为正例的可能性, 则比例

$$\frac{Y}{1 - Y}, \qquad \ln\frac{Y}{1 - Y}$$

分别称作 $Y$ 的几率 (odds) 和对数几率 (logit). 若把 $Y$ 展开成后验概率的形式 $\Pr(Y = 1 \mid \boldsymbol x)$, 则模型可以重写为

$$\ln \frac{\Pr(Y = 1 \mid \boldsymbol x)}{\Pr(Y = 0 \mid \boldsymbol x)} = \boldsymbol \beta^T \tilde{\boldsymbol x}$$

可以解出来

$$\Pr(Y = 1 \mid \boldsymbol x) = \frac{e^{\boldsymbol \beta^T \tilde{\boldsymbol x}}}{1 + e^{\boldsymbol \beta^T \tilde{\boldsymbol x}}}, \qquad \Pr(Y = 0 \mid \boldsymbol x) = \frac{1}{1 + e^{\boldsymbol \beta^T \tilde{\boldsymbol x}}}$$

所以给定 $\boldsymbol x$ 后, $Y$ 服从两点分布. 它的分布列是

$$p(y \mid \boldsymbol x) = \left( \frac{e^{\boldsymbol \beta^T \tilde{\boldsymbol x}}}{1 + e^{\boldsymbol \beta^T \tilde{\boldsymbol x}}} \right)^{y_i} \cdot \left( \frac{1}{1 + e^{\boldsymbol \beta^T \tilde{\boldsymbol x}}} \right)^{1 - y_i}$$

考虑极大似然估计. 已知数据集的情况下, 对数似然函数是

$$\ell(\boldsymbol \beta) = \sum _{i=1}^m \ln p(y_i \mid \boldsymbol x_i) = \sum _{i=1}^m \Bigg( \ln(1 + e^{\boldsymbol \beta ^T \tilde{\boldsymbol x_i}}) - y_i \boldsymbol \beta ^T \tilde{\boldsymbol x_i} \Bigg)$$

它的梯度和 Hessian 矩阵 分别是

$$\nabla \ell(\boldsymbol \beta) = -\sum _{i=1}^m \tilde{\boldsymbol x_i}\left( y_i - \frac{e^{\boldsymbol \beta^T \tilde{\boldsymbol x_i}}}{1 + e^{\boldsymbol \beta^T \tilde{\boldsymbol x_i}}} \right), \qquad \nabla ^2\ell(\boldsymbol \beta) = \sum _{i=1}^m \left( \boldsymbol x_i \boldsymbol x_i^T \cdot \frac{e^{\boldsymbol \beta^T \tilde{\boldsymbol x_i}}}{1 + e^{\boldsymbol \beta^T \tilde{\boldsymbol x_i}}} \cdot \frac{1}{1 + e^{\boldsymbol \beta^T \tilde{\boldsymbol x_i}}} \right)$$

使用 Newton 法迭代求解极值点, 迭代公式是

$$\boldsymbol \beta \gets \boldsymbol \beta - \Big(\nabla ^2 \ell(\boldsymbol \beta)\Big) ^{-1} \nabla \ell (\boldsymbol \beta)$$

  Logistic 回归也可以理解为是相互独立的 0-1 分布的参数估计, 其待估参数为 $\boldsymbol \beta$:

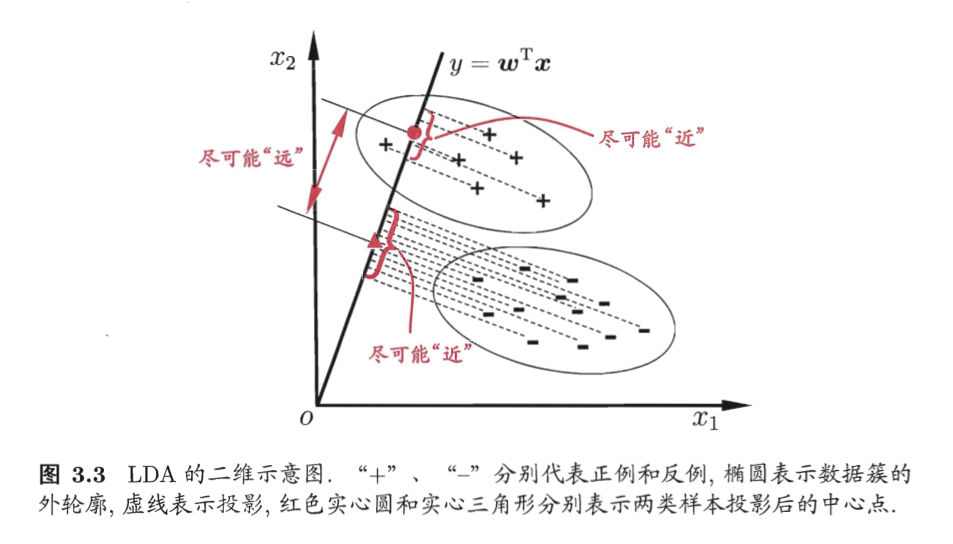
$$y_i \overset{\text{ind}}{\sim} p(\boldsymbol \beta ^T \tilde{\boldsymbol x}_i)$$

3.4 线性判别分析 LDA

  假设有一个二分类数据集 $D = \{(\boldsymbol x_i, y_i)\} _{i=1}^m, y_i \in \mathbb B$. 线性判别分析 (LDA, linear discriminant analysis) 是设法找到一条直线, 将样例投影到直线上, 并使同类投影点尽可能接近、异类尽可能远离.

  将正例和反例分成两个类 $X_k = \{\boldsymbol x_i: y_i = k\}, k\in \mathbb B$. 定义每个类的均值 $\boldsymbol \mu _k = \sum _{\boldsymbol x \in X _k}\boldsymbol x / |X_k|$. 首先考虑刻画类内点的距离, 考虑

$$s_{\rm w}^2 = \sum _{k \in \mathbb B} \sum _{\boldsymbol x \in X_k}\Big| \boldsymbol w ^T (\boldsymbol x - \boldsymbol \mu _k) \Big| ^2$$

是每类中每个点与该类均值距离投影的平方和. 然后考虑刻画类间距离, 考虑

$$s_{\rm b}^2 = \Big|\boldsymbol w ^T(\boldsymbol \mu _0 - \boldsymbol \mu _1)\Big| ^2$$

是两类均值点距离投影的平方. 同时考虑二者, 得到优化目标 $J = s_{\rm b}^2/s_{\rm w}^2 = \max$.

  现在用方差分析的语言重写这个优化目标. 定义类内散度矩阵 (within-class scatter matrix) 和类间散度矩阵 (between-class scatter matrix)

$$S_{\rm w} = \sum _{k \in \mathbb B} \sum _{\boldsymbol x \in X _k}(\boldsymbol x - \boldsymbol \mu _k)(\boldsymbol x - \boldsymbol \mu _k) ^T, \qquad S_{\rm b} = (\boldsymbol \mu _0 - \boldsymbol \mu _1)(\boldsymbol \mu _0 - \boldsymbol \mu _1) ^T$$

再定义全局散度矩阵

$$S_{\rm t} = \sum _{k \in \mathbb B} \sum _{\boldsymbol x \in X_i} (\boldsymbol x - \boldsymbol \mu)(\boldsymbol x - \boldsymbol \mu)^T$$

其中 $\boldsymbol \mu _k = \sum _{k \in \mathbb B} \sum _{\boldsymbol x \in X _k}\boldsymbol x / m$ 是所有点的均值. 全局散度矩阵可以分解为类内散度矩阵和类间散度矩阵之和

$$S_{\rm t} = S_{\rm w} + S_{\rm b}$$

  于是可以重写优化目标

$$J = \frac{\boldsymbol w ^TS_{\rm b}\boldsymbol w}{\boldsymbol w^TS_{\rm w}\boldsymbol w} = \max$$

即 $S_{\rm b}$ 与 $S_{\rm w}$ 的广义 Rayleigh 商. 由于我们只关注 $\boldsymbol w$ 的方向, 所以不失一般性, 限定 $\boldsymbol w^TS_{\rm w}\boldsymbol w = 1$. 求解最优化问题

$$\begin{aligned} \max _{\boldsymbol w} \quad & \boldsymbol w^TS_{\rm b}\boldsymbol w\\ \text{s.t.} \quad & \boldsymbol w^TS_{\rm w}\boldsymbol w = 1 \end{aligned}$$

使用 Lagrange 乘子法. 它的 Lagrange 函数是

$$\mathcal L(\boldsymbol w, \lambda) = -\boldsymbol w^TS_{\rm b}\boldsymbol w + \lambda (\boldsymbol w^TS_{\rm w}\boldsymbol w - 1)$$

令导数为零

$$\frac{\partial \mathcal L}{\partial \boldsymbol w} = -2S_{\rm b}\boldsymbol w + 2\lambda S_{\rm w}\boldsymbol w = 0 \implies S_{\rm b}\boldsymbol w = \lambda S_{\rm w}\boldsymbol w$$

我们只要得到其中一组解就可以了. 注意到

$$S_{\rm b} \boldsymbol w = (\boldsymbol \mu _0 - \boldsymbol \mu _1)(\boldsymbol \mu _0 - \boldsymbol \mu _1) ^T \boldsymbol w$$

这启发我们令 $\lambda = (\boldsymbol \mu _0 - \boldsymbol \mu _1) ^T \boldsymbol w$. 此时有

$$S_{\rm b} \boldsymbol w = \lambda (\boldsymbol \mu _0 - \boldsymbol \mu _1)$$

代入 $S_{\rm b}\boldsymbol w = \lambda S_{\rm w}\boldsymbol w$ 得到一组解

$$\boldsymbol w = S_{\rm w}^{-1}(\boldsymbol \mu _0 - \boldsymbol \mu _1), \quad \lambda = (\boldsymbol \mu _0 - \boldsymbol \mu _1) ^T \boldsymbol w$$

  在多分类问题中 $k \in \{1, \dots, N\}$ 而不是 $\mathbb B$. 此时重新定义

$$S_{{\rm w}k} = \sum _{\boldsymbol x \in X _k}(\boldsymbol x - \boldsymbol \mu _k)(\boldsymbol x - \boldsymbol \mu _k) ^T, \quad S_{\rm w} = \sum _k S_{{\rm w}k}, \qquad S_{\rm b} = \sum _{i=1}^N|X_i|(\boldsymbol \mu _i - \boldsymbol \mu)(\boldsymbol \mu _i - \boldsymbol \mu)^T$$

此时优化问题为

$$\max _{W \in \mathbb R ^{d \times (N-1)}} \frac{\mathop{\rm tr}W^TS_{\rm b}W}{\mathop{\rm tr}W^TS_{\rm w}W}$$

该问题可化为广义特征值问题

$$S_{\rm b}W = \lambda S_{\rm w}W$$

组合其前 $N-1$ 个最大特征值对应的特征向量即可得到 $W$ 的解.

3.5 多分类问题

  本节研究如何将二分类问题推广至多分类. 使用拆解法, 将多分类问题拆解为若干个二分类问题. 假设数据集 $D = \{(\boldsymbol x_i, y_i)\} _{i=1}^m, y_i \in \{C_1, \dots, C_N\}$ 常见的拆解方法有三种:

1. 一对一 (OvO, one vs one), 每次将其中一类作为正例、另外其中一类作为反例, 拆解为 $O(N^2)$ 个规模为 $O(m/N)$ 的二分类问题;

2. 一对其余 (OvR, one vs rest), 每次将其中一类作为正例、其它所有类作为反例, 拆解为 $O(N)$ 个规模为 $(m)$ 的二分类问题;

3. 多对多 (MvM, many vs many), 每次将若干类作为正例、其他所有类作为反例, 正反例构造必须有特殊设计, 不能随意选取.

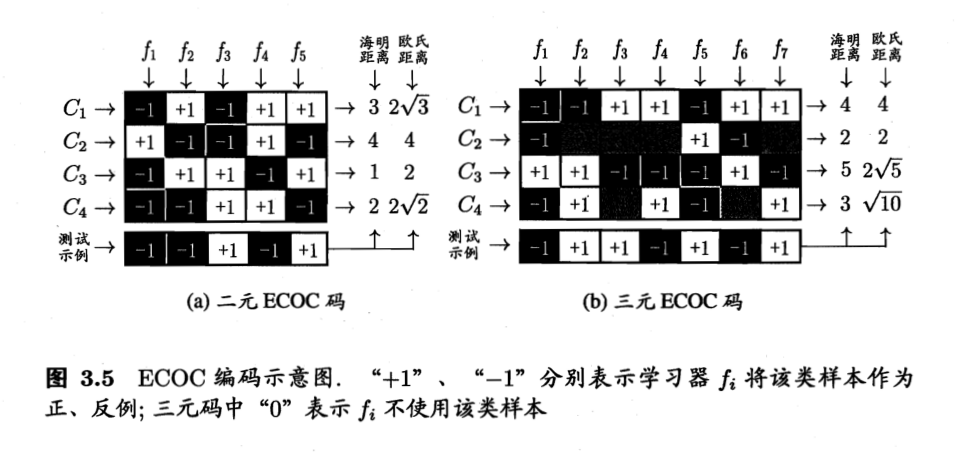
  纠错输出码 (ECOC, error correcting output codes) 是一种常见的 MvM 技术. 预设分类器数量 $M$, 先给每一个分类器安排正反例, 并统计每一个类别 $C_i$ 在每一个分类器的正反例情况 $\boldsymbol C_i \in \mathbb B ^M$. 统计测试用例在每个分类器的分类结果 $\boldsymbol C^*$, 并选择距离最近的那个 $\boldsymbol C_i$ 作为最终结果.

3.6 类别不平衡问题

  有时正例数量远远少于反例. 解决类别不平衡问题的常见方法有三种:

1. 欠采样 (undersampling), 即舍弃一些反例;

2. 过采样 (oversampling), 即增加一些正例;

3. 阈值移动 (threshold-moving).

  阈值移动的一个基本策略是再缩放 (rescaling). 例如线性分类器考虑了 $y / (1 - y) > 1$ 时预测为正例. 当正反例数量不同时, 应该用 $|X_1| / |X_0|$ 作为阈值而不是用 $1$.

本系列的参考文献

[1] 周志华. 机器学习[M]. 清华大学出版社, 2016.

[2] 谢文睿, 秦州, 贾彬彬. 机器学习公式详解[M]. 人民邮电出版社, 2023.