《机器学习》笔记（第二部分：决策树、神经网络、支持向量机）

4 决策树

4.1 基本流程

  假设数据集 $D = \{(\boldsymbol x_i, y_i)\}_{i=1}^m$, $\boldsymbol x_i = (x_{ij})_{j=1}^d$, 属性序号集 $A = \{a\}_{a=1}^d$.

  问题: 生成一棵树. 深度为 $d + 1$, 其中根节点和中间节点共 $d$ 层, 结果叶节点 $1$ 层. 每个根 (中间) 节点是一个决策: 属性 $a_*$ 的值是多少? 根据其取值, 确定下一轮进入的子节点. 从根节点往下判断, 共经过 $d$ 个节点, 恰好是全部 $d$ 个属性的问题.

• 函数 generate_tree($D$, $A$)
• 输入:
  • 训练集 $D = \{(\boldsymbol x_i, y_i)\}_{i=1}^m$
  • 属性序号集 $A = \{a\}_{a=1}^d$
• 过程:
  1. 生成节点 node
  2. if $y_1 = y_2 = \cdots = y_m$
  3.   将 node 标记为叶节点, 其类别为 $y_1$
  4. if $\boldsymbol x_1 = \boldsymbol x_2 = \cdots = \boldsymbol x_m$
  5.   将 node 标记为叶节点, 其类别为 $\{y_i\}$ 的众数
  6. 从 $A$ 中选择一个最优划分属性 $a^*$
  7. for $a^*$ 的每一种可能取值 $v$
  8.   为 node 生成一个分支节点 subnode
  9.   令 $D_v$ 表示 $D$ 中在 $a^*$ 取值为 $v$ 的样本子集
  10.   if $D_v = \varnothing$
  11.     将 subnode 标记为叶节点, 其类别为 $\{y_i\}$ 的众数
  12.   else
  13.     令 subnode 为 generate_tree($D_v$, $A \setminus \{a^*\}$)

这样可以生成一个深度最多为 $d + 1$ 的树.

4.2 划分选择

  问题: 在当前给定的数据集 $D$ 和属性集 $A$ 下, 在当前节点 node 处, 应该选择哪一个属性作为最优划分属性? 选定优化目标: 我们希望每个 subnode 所包含的样本, 尽可能属于同一类别. 即纯度 (purity) 越来越高.

信息熵 对于这个问题, Shannon 已经给了我们答案. 对于数据集 $D$, 定义信息熵 (information entropy)

$$\mathop{\rm Ent} D := - \sum _{y \in \mathcal Y} p_y \mathop{\mathrm{lb}} p_y$$

其中 $\mathcal Y$ 是标记集, $p_y$ 表示标记值为 $y$ 的样本占整个 $D$ 的比例. 约定 $0 \mathop{\mathrm{lb}} 0 = 0$. 它的取值范围是

$$0 \leq \mathop{\rm Ent} D \leq \mathop{\mathrm{lb}} |\mathcal Y|$$

我们的目的是降低信息熵: 信息熵越小, $D$ 的纯度越高.

信息增益 给定属性 $a^*$, 考虑划分前与划分后信息熵之差 (加权)

$$\mathop{\rm Gain} _D a^* := \mathop{\rm Ent} D - \sum _{v \in \mathcal X_{a^*}} \frac{|D_v|}{|D|} \mathop{\rm Ent} D_v$$

其中 $v$ 取遍属性 $a^*$ 的所有可能取值, $D_v$ 表示 $D$ 中在 $a^*$ 取值为 $v$ 的样本子集. 上面的差式定义为信息增益 (information gain). 差式越大, 说明 $a^*$ 在划分 $D$ 式造成的信息熵减少越多. 故取

$$a^* = {\arg \max} _{a \in A} \mathop{\rm Gain} _D a$$

作为划分属性即可.

增益率 信息增益有一个漏洞, 它偏好取值种类较多的属性. 作为一个修正, 定义增益率 (gain ratio)

$$\mathop{\rm GainRatio} _D a := \frac{\mathop{\rm Gain} _D a}{\mathop{\rm IV} _D a}, \qquad \mathop{\rm IV} _D a := - \sum _{v \in \mathcal X_{a^*}} \frac{|D_v|}{|D|} \mathop{\mathrm{lb}} \frac{|D_v|}{|D|}$$

其中 $\mathop{\rm IV} _D a$ 是属性 $a$ 在训练集 $D$ 上的固有值 (intrinsic value). 增益率偏好取值种类较少的属性.

基尼指数 基尼指数 (Gini index) 反映了数据集中任取两个样本, 其类别标记不一致的概率. 定义基尼值 (Gini value)

$$\mathop{\rm Gini} D := \sum _{\substack{y, y' \in \mathcal Y\\ y \neq y'}} p_y p_{y'} = 1 - \sum _{y \in \mathcal Y} p_y^2$$

基尼指数越小, 数据集纯度越高. 定义基尼指数

$$\mathop{\rm GiniIndex} _D a := \sum _{v \in \mathcal X_{a^*}} \frac{|D_v|}{|D|} \mathop{\rm Gini} D_v$$

取基尼指数最小的那个属性

$$a^* = {\arg \min} _{a \in A} \mathop{\rm GiniIndex} _D a$$

作为划分属性即可.

4.3 剪枝处理

  完整的、将每一个属性都完全划分的决策树, 很容易出现过拟合问题. 对于每一个节点 node, 比较剪枝前 (即 node 是有分支的节点) 和剪枝后 (即将 node 置为叶子结点), 决策树在验证集 $T$ 的预测精度, 来决定是否要进行剪枝操作.

预剪枝 在生成决策树时, 若当前节点 node 划分后比划分前预测精度低, 则将 node 置为叶节点. 其类别为 $y_i$ 的众数. 预剪枝是基于贪心思想设计, 容易欠拟合.

后剪枝 在生成完决策树后, 从叶节点往上逐个判断. 若节点 node 划分后精度反低, 则置为叶节点. 后剪枝有效规避了欠拟合问题, 但是计算开销较大.

4.4 连续与缺失值

4.4.1 连续值处理

  研究属性 $a \in A$ 是连续值的情况, 即 $\mathcal X_a$ 是连续的. 基本思想是将属性 $a$ 通过阈值 $t \in \mathbb R$ 分为正反两类. 假设样本集 $D$ 在属性 $a$ 上有 $n$ 个取值 $\{v_{(i)}\}_{i=1}^n$ (从小到大排序), 从以下集合中选取阈值 $t$

$$t \in T = \left\{ \frac{v_{(i)} + v_{(i+1)}}{2} \right\}_{i=1}^{n-1}$$

选取后, 按照样本在属性 $a$ 上取值大于 $t$ 和小于 $t$ 分为两个集合, 记为

$$D = D^+ \cup D^-, \qquad D^+ \cap D^- = \varnothing$$

该属性的增益值为取遍所有可能的 $t$ 造成的增益的最大值, 即

$$\mathop{\rm Gain} _D a^* := \mathop{\rm Ent} D - \frac{|D^+|}{|D|} \mathop{\rm Ent} D^+ - \frac{|D^-|}{|D|} \mathop{\rm Ent} D^-$$

需要注意的是, 若当前划分属性是连续属性, 则该属性还可作为其后代节点的划分属性. 此时树的深度可能大于 $d + 1$.

4.4.2 缺失值处理

  研究属性 $a \in A$ 有缺失值的情况. 首先考虑如何选择划分准则. 记 $\tilde D$ 为属性 $a$ 没有缺失值的样本子集, $\tilde D_v$ 为 $\tilde D$ 中在属性 $a$ 取值 $v$ 的样本子集. 为每一个样本 $\boldsymbol x_i$ 赋予一个初始权重 $w_i = 1$. 定义

$$\rho := \sum _{\substack{i=1\\ \boldsymbol x_i \in \tilde D}}^n w_i \Bigg/ \sum _{i=1}^n w_i, \qquad r_v := \sum _{\substack{i=1\\\boldsymbol x_i \in \tilde D_v}}^n w_i \Bigg/ \sum _{\substack{i=1\\ \boldsymbol x_i \in \tilde D}}^n w_i$$

$\rho$ 表示无缺失值样本占比; $r_v$ 表示无缺失样本中属性 $a$ 的值为 $v$ 的样本占比. 信息增益推广为

$$\mathop{\rm Gain} _D a := \rho \left( \mathop{\rm Ent} \tilde D - \sum _{v \in \mathcal X_a} r_v \mathop{\rm Ent} \tilde D_v \right)$$

  再考虑选定划分属性 $a$ 后如何对样本进行划分. 若 $x_ia$ 已知, 则正常生成节点并将 $\boldsymbol x_i$ 放入该节点. 若 $x_ia$ 缺失, 则将 $\boldsymbol x_i$ 同时划入所有子节点, 且样本权值在属性值为 $v$ 的子节点中调整为 $r_v w_i$. 这是将 $\boldsymbol x_i$ 以不同概率分入不同子节点中.

4.5 多变量决策树

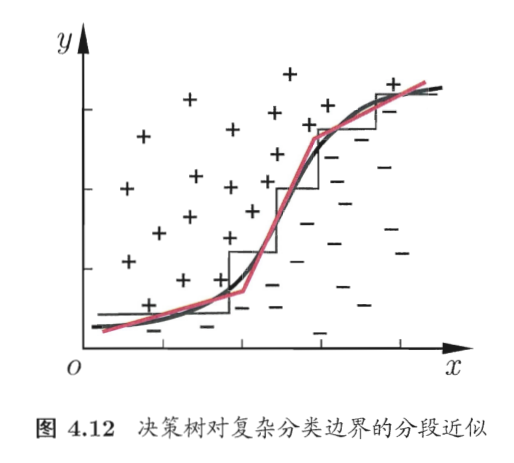
  前面说的是单变量决策树, 即每一节点只根据一个属性的值分类, 分类边界在图上画出来是与坐标轴平行的折线段. 多变量决策树 (multivariate decision tree) 的节点根据多个属性的线性组合的值分类, 这样可以形成斜的分类边界.

5 神经网络

5.1 神经元模型

  神经元 (neuron) 是神经网络的基本单位. 它由 $n$ 个输入 $\{x_i\}_{i=1}^n$、$n$ 个权重 $\{w_i\}_{i=1}^n$、一个阈值 (threshold) $\theta \in \mathbb R$ 和一个激活函数 (activation function) $f: \mathbb R \to \mathbb R$ 计算输出 $y$

$$y = f\left(\sum _{i=1} ^n w_i x_i - \theta \right)$$

其中激活函数 $f$ 有一些常见取法, 例如阶跃函数

$$f: \mathbb R \to \{0, 1\}, \quad x \mapsto \mathit 1_{x \geq 0}$$

例如 ReLU 函数

$$f: \mathbb R \to [0, +\infty), \quad x \mapsto \mathit 1_{x \geq 0} \cdot x$$

再例如 Sigmoid 函数

$$f: \mathbb R \to (0, 1), \quad x \mapsto \frac{1}{1 + e^{-x}}$$

Sigmoid 函数是可导的. 它的导数是

$$f'(x) = f(x)(1-f(x))$$

5.2 感知机

  感知机 (perceptron) 就是 $2$ 层共 $n+1$ 个神经元构成的神经网络: 输入层 ($n$ 个神经元) 和输出层 ($1$ 个神经元). 取激活函数为阶跃函数 $f(x) = \mathit 1 _{x \geq 0}$, 输出 $y$ 与输入 $\{x_i\}_{i=1}^n$ 的对应关系是

$$y = f\left( \sum _{i=1} ^n w_i x_i - \theta \right) = \begin{cases} 1, & \sum w_i x_i \geq \theta, \\ 0, & \sum w_i x_i < \theta \end{cases}$$

这在几何上等价于在 $\mathbb R ^n$ 中用一个 $n-1$ 维超平面将全空间分割为两部分, 一部分输出为 $1$ 而另一部分为 $0$, 以此实现分类功能.

  记 $y$ 是真实值, $\hat y = f(\sum w_i x_i - \theta)$ 是预测值. 定义损失函数

$$L(w_1, \dots, w_n, \theta) = (\hat y - y)\left(\sum _{i=1}^n w_i x_i - \theta\right)$$

这是一个合理的损失函数, 因为正确分类点损失为 $0$; 错误分类点损失为正, 且与该点与超平面的距离正相关. 现在进行简化, 令 $w_{n+1} = \theta$ 和 $x_{n+1} = -1$, 即定义一个固定输入为 $-1$ 的哑结点 (dummy node). 此时损失函数简化为

$$L(w_1, \dots, w_n, w_{n+1}) = (\hat y - y) \sum _{i=1}^{n+1} w_i x_i = (\hat y - y) \boldsymbol w^T \boldsymbol x$$

其中 $\boldsymbol w = (w_i)_{i=1}^{n+1}$ 是权值向量, $\boldsymbol x = (x_i)_{i=1}^{n+1}$ 是输入向量.

  现在建立基于梯度下降的优化方法. 感知机使用随机梯度下降法: 每次随机选取一个误分类点 $(\boldsymbol x, y)$ 并进行下降. 求损失函数的梯度

$$\nabla L(\boldsymbol w) = (\hat y - y) \boldsymbol x$$

得到梯度下降的更新式

$$\boldsymbol w \gets \boldsymbol w + \Delta \boldsymbol w, \quad \Delta \boldsymbol w = - \eta (\hat y - y) \boldsymbol x$$

其中学习率 (learning rate) $\eta \in (0, 1)$ 是一个预设参数. 重复迭代直到收敛即可.

  感知机只有一层功能神经元 (functional neuron), 只可以处理线性可分 (linearly separable) 的问题. 处理更复杂的问题需要使用多层网络.

5.3 多层网络与误差逆传播算法

5.3.1 信号的前向传播

  假设一个包含 $1$ 个隐藏层 (hidden layer) 的神经网络. 给定训练集 $D = \{(\boldsymbol x_i, \boldsymbol y_i)\}_{i=1}^m, \boldsymbol x_i \in \mathbb R^d, \boldsymbol y_i \in \mathbb R^\ell$, 注意这里输入和输出都是向量.

  约定符号:

• 输入层:
  • 有 $d$ 个神经元;
  • 第 $i$ 个神经元的输入是 $x_i$.
• 输入层第 $i$ 个神经元至隐藏层第 $h$ 个神经元的连接权重是 $v_{ih}$;
• 隐藏层:
  • 有 $q$ 个神经元;
  • 第 $h$ 个神经元的输入是 $\alpha _h$, 阈值是 $\gamma _h$, 输出是 $b_h$.
• 隐藏层第 $h$ 个神经元至输出层第 $j$ 个神经元的连接权重是 $w_{ih}$;
• 输出层:
  • 有 $\ell$ 个神经元;
  • 第 $j$ 个神经元的输入是 $\beta _j$, 阈值是 $\theta _j$, 输出是 $y_j$.

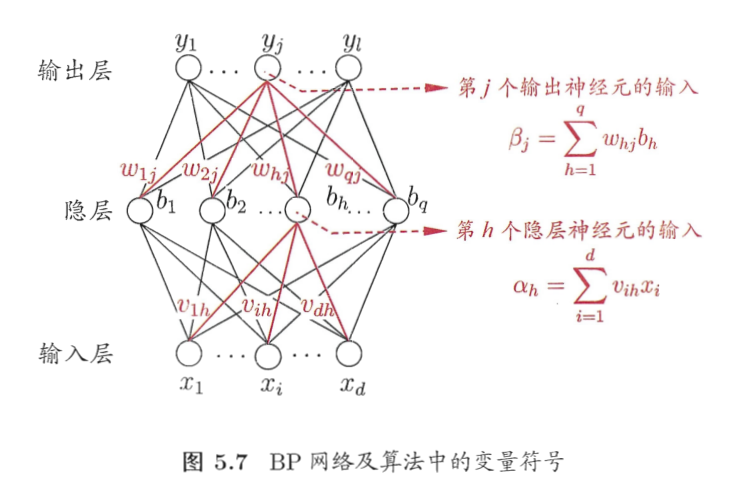
它们的联系是:

$$\alpha _h = \sum _{i=1}^d v_{ih} x_i, \qquad b_h = f(\alpha _h - \gamma _h)$$

以及

$$\beta _j = \sum _{h=1}^q w_{hj} b_h, \qquad y_j = f(\beta _j - \theta _j)$$

  该神经网络的参数有

$$\mathcal W = \{v_{ih}\}_{i \leq d, h \leq q} \cup \{\gamma _h\}_{h \leq q} \cup \{w_{hj}\}_{h \leq q, j \leq \ell} \cup \{\theta _j\}_{j \leq \ell}$$

共 $(d + 1)q + (q + 1)j$ 个.

5.3.2 误差的反向传播

  以均方误差作为优化目标:

$$E = \frac 12 ||\hat{\boldsymbol y} - \boldsymbol y|| _2^2 = \min$$

选定 $f$ 是 Sigmoid 函数, 对 $w_{hj}$ 求导:

$$\frac{\partial E}{\partial w_{hj}} = \frac{\partial E}{\partial \hat y_j} \cdot \frac{\partial \hat y_j}{\partial \beta _j} \cdot \frac{\partial \beta _j}{\partial w_{hj}}$$

定义输出层神经元的梯度 $g_j$

$$g_j := -\frac{\partial E}{\partial \hat y_j} \cdot \frac{\partial \hat y_j}{\partial \beta _j} = (\hat y_j - y_j) \cdot \hat y_j (1 - \hat y_j)$$

于是有

$$\Delta w_{hj} = -\eta \frac{\partial E}{\partial w_{hj}} = \eta g_j b_h$$

类似可得

$$\Delta \theta _j = -\eta g_j, \quad \Delta v_{ih} = \eta e_h x_i, \quad \Delta \gamma _h = -\eta e_h$$

其中隐藏层神经元的梯度 $e_h$

$$e_h := -\frac{\partial E}{\partial b_h} \cdot \frac{\partial b_h}{\partial \alpha _h} = \left(\sum _{j=1}^\ell w_{hj}g_j\right) \cdot b_h (1 - b_h)$$

所有的导数都有显式解.

  误差逆传播 (error backpropagation) 算法流程如下:

• 输入:
  • 训练集 $D = \{(\boldsymbol x_k, y_k)\}_{k=1}^m$
  • 超参数:
    • 学习率 $\eta$
• 过程:
  1. 随机生成权值和阈值的初值 $w_{hj}, \theta _j, v_{ih}, \gamma _h \in (0, 1)$
  2. do until 收敛或达到最大迭代次数
  3.   for each $(\boldsymbol x, \boldsymbol y) \in D$ do
  4.     根据当前参数计算输出 $\boldsymbol y$ (信号的前向传播)
  5.     计算输出层神经元梯度 $g_j$
  6.     计算隐藏层神经元梯度 $e_h$
  7.     更新权值和阈值 $w_{hj}, \theta _j, v_{ih}, \gamma _h$ (误差的反向传播)

  多层神经网络可以拟合任意复杂的连续函数, 但是常遭遇过拟合. 常用的有两种方法: 一是早停 (early stopping), 即若训练集误差降低但验证集误差升高则停止训练; 二是正则化 (regularization), 即误差函数同时考虑误差的大小和权值的大小

$$\tilde E = \lambda E + (1 - \lambda) \sum _{w \in \mathcal W} w^2$$

其中 $w$ 取遍所有权值和阈值.

6 支持向量机 SVM

6.1 间隔与支持向量

  给定训练样本集 $D = \{(\boldsymbol x_i, y_i)\}_{i=1}^m, \boldsymbol x \in \mathbb R^n, y_i \in \mathbb B$. 寻找一个超平面 $\ell : \boldsymbol w^T \boldsymbol x + b = 0$, 使得超平面的分类效果最好.

  考虑两个超平面, 将全空间分为三个部分:

• $\ell ^+ : \boldsymbol w^T \boldsymbol x + b = +1$, 所有正例在其之外, 最近的正例在其之上 (称为正支持向量);
• $\ell ^- : \boldsymbol w^T \boldsymbol x + b = -1$, 所有反例在其之外, 最近的反例在其之上 (称为反支持向量);
• $\ell ^+$ 与 $\ell ^-$ 之间有距离为 $\gamma = 2/|\boldsymbol w|$ 无样例区域.

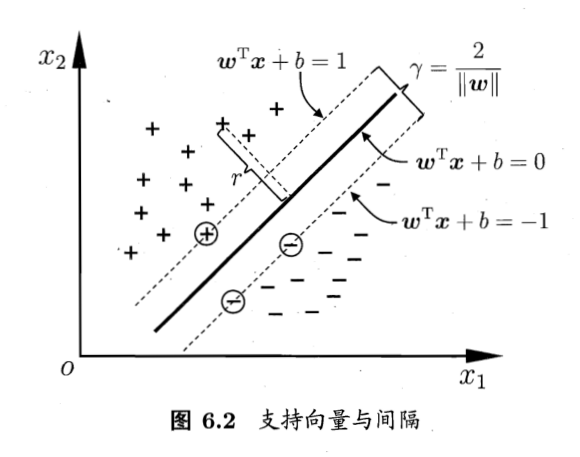
  即是说在

$$\begin{cases} \boldsymbol w^T \boldsymbol x_i + b \geq +1, \quad & y_i = +1\\ \boldsymbol w^T \boldsymbol x_i + b \leq -1, \quad & y_i = -1 \end{cases}$$

的条件下使得间隔最大

$$\max \gamma = \frac{2}{|\boldsymbol w|} \quad \iff \quad \min \frac 12 |\boldsymbol w| ^2$$

所以支持向量机的优化目标是

$$\begin{aligned} \min _{\boldsymbol w, b} \quad & \frac{1}{2} |\boldsymbol w|^2\\ \text{s.t.} \quad & y_i(\boldsymbol w^T \boldsymbol x_i + b) \geq 1, \forall i \end{aligned}$$

6.2 对偶问题

  考虑 Lagrange 乘子法. 它的 Lagrange 函数是

$$\mathcal L(\boldsymbol w, b, \boldsymbol \alpha) = \frac 12 |\boldsymbol w| ^2 + \sum_{i=1}^m a_i (1 - y_i(\boldsymbol w ^T \boldsymbol x + b))$$

其中 $\boldsymbol \alpha = (\alpha _1, \dots, \alpha _m)$ 是 Lagrange 乘子. $\alpha _i > 0, \forall i$.

  Lagrange 乘子法就是将求目标函数条件最值的问题转化为求 Lagrange 函数全局最值的问题. 现求解 $\max \mathcal L$: 对 $\boldsymbol w$ 和 $b$ 求导并令导数为 $\boldsymbol 0$ 和 $0$, 得到

$$\sum _{i=1}^m \alpha _i y _i \boldsymbol x _i = \boldsymbol w, \qquad \sum _{i=1}^m \alpha _i y _i = 0$$

将第一式代入 Lagrange 函数可消去 $\boldsymbol w$ 和 $b$

$$\mathcal L = \sum _{i=1}^m \alpha _i - \frac 12\sum _{i=1}^m \sum _{j=1}^m \alpha _i \alpha _j y_i y_j \boldsymbol x _i^T \boldsymbol x_j$$

将 Lagrange 乘子看做自变量, 得到一个仅关于 $\alpha _i$ 的对偶问题

$$\begin{aligned} \max _{\boldsymbol \alpha} \quad & \sum _{i=1}^m \alpha _i - \frac 12\sum _{i=1}^m \sum _{j=1}^m \alpha _i \alpha _j y_i y_j \boldsymbol x _i^T \boldsymbol x_j\\ \text{s.t.} \quad & \sum _{i=1}^m \alpha _i y_i = 0, \\ & \alpha _i \geq 0, \forall i \end{aligned}$$

KKT 条件是最优化问题的必要条件. 据其有

$$\forall i, \alpha _i = 0 \lor y_i (\boldsymbol w ^T \boldsymbol x_i + b) = 1$$

所以样本点 $(\boldsymbol x_i, y_i)$ 要么对划分超平面的选取没有影响 (因为 $\alpha _i = 0$ 而 $w = \sum \alpha _i y_i \boldsymbol x_i$); 要么在 $\ell ^+$ 或 $\ell ^-$ 上, 此时该样本点是支持向量. 亦即划分平面的选取仅与支持向量有关.

  上面的最优化问题有 $m$ 个待求解变量 $\alpha _i$, 自由度为 $m - 1$. 求解使用 SMO (Sequential Minimal Optimization) 算法求解:

• 选取一对样本 $(\boldsymbol x_i, y_i), (\boldsymbol x_j, y_j)$, 一般使用违背 KKT 条件程度最大的一对样本;
• 固定 $\alpha _i$ 和 $\alpha _j$ 以外的其它参数, 求解上面的最优化问题 (此时已简化为一个一元二次最值问题), 更新 $\alpha _i, \alpha _j$ 的值;
• 不断重复上述两步直到收敛.

  在获得所有 $\alpha _i$ 的值后, 就可以确定 $\boldsymbol w = \sum \alpha _i y_i \boldsymbol x_i$ 以及 $b = y_s - \sum \alpha _i y_i \boldsymbol x _i^T \boldsymbol x_s$, 其中 $s$ 取任意支持向量 $(\boldsymbol x_s, y_s)$.

6.3 核函数

  有定理表明: 若样本维数 $d < \infty$, 则存在一个升维的函数 $\varphi: \mathbb R^d \to \mathbb R^{d'} (d' > d)$, 使得映射后的样本集 $D' = \{(\varphi(\boldsymbol x_i), y_i)\}_{i=1}^m$ 是线性可分的. 希望找到一个超平面 $\boldsymbol w^T \varphi(\boldsymbol x) + b = 0$. 优化问题是

$$\begin{aligned} \min _{\boldsymbol w, b} \quad & \frac{1}{2} |\boldsymbol w|^2\\ \text{s.t.} \quad & y_i(\boldsymbol w^T \varphi(\boldsymbol x_i) + b) \geq 1, \forall i \end{aligned}$$

对偶问题是

$$\begin{aligned} \max _{\boldsymbol \alpha} \quad & \sum _{i=1}^m \alpha _i - \frac 12\sum _{i=1}^m \sum _{j=1}^m \alpha _i \alpha _j y_i y_j \varphi(\boldsymbol x _i)^T \varphi(\boldsymbol x_j)\\ \text{s.t.} \quad & \sum _{i=1}^m \alpha _i y_i = 0, \\ & \alpha _i \geq 0, \forall i \end{aligned}$$

其中 $\varphi(\boldsymbol x_i)^T \varphi(\boldsymbol x_j)$ 是 $\varphi : \mathbb R^d \to \mathbb R^{d'}$ 与 $(\cdot)^T(\cdot) : \mathbb R^{d'} \times \mathbb R^{d'} \to \mathbb R$ 的复合. 为了规避 $d'$ 维空间, 定义这个复合为核函数 (kernel function) $\kappa : \mathbb R^d \times \mathbb R^d \to \mathbb R$. 对于核函数的选取有如下定理:

核函数定理 给定数据集 $D = \{\boldsymbol x_i\}_{i=1}^m$, 对称函数 $\kappa : \mathbb R^d \times \mathbb R^d \to \mathbb R$ 是核函数当且仅当其核矩阵 (kernel matrix) 半正定.

$$K := \begin{pmatrix} \kappa(\boldsymbol x_1, \boldsymbol x_1) & \cdots & \kappa(\boldsymbol x_1, \boldsymbol x_m)\\ \vdots & \ddots & \vdots\\ \kappa(\boldsymbol x_m, \boldsymbol x_1) & \cdots & \kappa(\boldsymbol x_m, \boldsymbol x_m) \end{pmatrix} \succeq 0$$

  核函数的选择对支持向量机的性能至关重要. 常见的核函数有:

核函数	表达式	参数
线性核	$\kappa (\boldsymbol x_i, \boldsymbol x_j) = \boldsymbol x_i^T \boldsymbol x_j$	-
多项式核	$\kappa (\boldsymbol x_i, \boldsymbol x_j) = (\boldsymbol x_i^T \boldsymbol x_j) ^d$	$d \geq 1$ 是多项式次数
RBF (Gauss) 核	$\kappa (\boldsymbol x_i, \boldsymbol x_j) = \exp -\|\boldsymbol x_i - \boldsymbol x_j\|^2 / 2\sigma^2$	$\sigma > 0$ 是 Gauss 核的带宽 (width)
Laplace 核	$\kappa (\boldsymbol x_i, \boldsymbol x_j) = \exp -\|\boldsymbol x_i - \boldsymbol x_j\| / \sigma$	$\sigma > 0$
Sigmoid 核	$\kappa (\boldsymbol x_i, \boldsymbol x_j) = \tanh (\beta \boldsymbol x_i^T \boldsymbol x_j - \theta)$	$\beta > 0, \theta > 0$

此外, 核函数还可以通过组合得到.

• 核函数的线性组合是核函数;
• 核函数的积是核函数;
• 对于核函数 $\kappa$ 和任意函数 $g(\cdot)$, $g(\boldsymbol x_i) \kappa(\boldsymbol x_i, \boldsymbol x_j) g(\boldsymbol x_j)$ 是核函数.

6.4 软间隔与正则化

  求解划分平面时, 可以不要求所有样本都划分正确. 称为划分可以具有软间隔 (soft margin). 在优化目标中加入一个惩罚项:

$$\min _{\boldsymbol w, b} \frac 12 |\boldsymbol w|^2 + C \cdot \sum _{i=1} ^m \ell (y_i (\boldsymbol w ^T \boldsymbol x _i + b) - 1)$$

其中 $\ell(z) = \mathit 1_{z<0}$ 是惩罚函数. 惩罚函数也可以选择其它函数, 例如 hinge 损失:

$$\ell(z) = \max (0, 1 - z)$$

此时优化问题可以重写为

$$\begin{aligned} \min _{\boldsymbol w, b, \boldsymbol \xi} \quad & \frac 12 |\boldsymbol w| ^2 + C \sum _{i=1} ^m \xi _i\\ \text{s.t.} \quad & y_i (\boldsymbol w^T \boldsymbol x_i + b) \geq 1 - \xi _i, \\ & \xi _i \geq 0, \forall i \end{aligned}$$

其中 $\boldsymbol \xi$ 称为松弛变量 (slack variables), 它是一个中间变量. 该问题的 Lagrange 函数是

$$\begin{aligned} \mathcal L (\boldsymbol w, n, \boldsymbol \alpha, \boldsymbol \xi, \boldsymbol \mu) = & \frac 12 |\boldsymbol w| ^2 + C \sum _{i=1} ^m \xi _i\\ & + \sum _{i=1} ^m \alpha _i (1 - \xi _i - y_i (\boldsymbol w^T \boldsymbol x_i + b)) - \sum _{i=1} ^m \mu _i \xi _i \end{aligned}$$

其中 $\alpha _i \geq 0, \mu _i \geq 0$ 是 Lagrange 乘子. 对 $\boldsymbol w, b, \boldsymbol \xi$ 求偏导并令其为零

$$\sum _{i=1} ^m \alpha _i y_i \boldsymbol x_i = \boldsymbol w, \qquad \sum _{i=1} ^m \alpha _i y_i = 0, \qquad \boldsymbol \alpha + \boldsymbol \mu = C \cdot \boldsymbol 1$$

它的对偶问题是

$$\begin{aligned} \max _{\boldsymbol \alpha} \quad & \sum _{i=1}^m \alpha _i - \frac 12\sum _{i=1}^m \sum _{j=1}^m \alpha _i \alpha _j y_i y_j \boldsymbol x _i^T \boldsymbol x_j\\ \text{s.t.} \quad & \sum _{i=1}^m \alpha _i y_i = 0, \\ & \alpha _i \geq 0 \geq C, \forall i \end{aligned}$$

比硬间隔多出一条 $\alpha _i \leq C$ 的限制, 可以用相同算法求解. 它的 KKT 条件中要求

$$\alpha _i = 0 \lor y_i (\boldsymbol w ^T \boldsymbol x + b) - 1 + \xi _i = 0, \qquad \mu _i = 0 \lor \xi _i = 0$$

即样本 $i$ 一方面要么对划分平面选取无影响, 要么是支持向量; 若是支持向量, 要么在两条最大间隔边界上 ($\xi _i = 0$), 要么在最大间隔边界之间 ($\mu _i = 0 \land 0 < \xi \leq 1$) 或者被错误分类 ($\mu _i = 0 \land \xi > 1$).

 假设划分超平面以 $f(\boldsymbol x, \boldsymbol \theta) = 0$ 的方程形式给出, 其中 $\boldsymbol x$ 是自变量, $\boldsymbol \theta$ 是参数. 假设划分的超平面的间隔是 $\Omega(\boldsymbol \theta)$, 样本 $(\boldsymbol x_i, y_i)$ 造成的惩罚是 $\ell(f(\boldsymbol x_i), y_i)$. 此时优化目标是

$$\min _{\boldsymbol \theta} \quad \Omega(\boldsymbol \theta) + C \cdot \sum _{i=1} ^m \ell(f(\boldsymbol x_i), y_i)$$

其中 $\Omega(\boldsymbol \theta)$ 称为结构风险 (structural risk), 与模型本身有关; $\sum \ell(f(\boldsymbol x_i), y_i)$ 称为经验风险 (empirical risk), 与模型同训练数据的契合程度有关.

  正则化 (regularization) 是一个机器学习术语, 指在原始模型中引入额外信息, 以防止过拟合并提高泛化性能. $\Omega(\boldsymbol \theta)$ 称为正则化项, $C$ 称为正则化常数. ${\rm L}_p$ 范数是常用的正则化项: $\rm L_2$ 范数倾向平衡各分量取值, $\rm L_1$ 与 $\rm L_0$ 范数倾向减少非零分量个数.

6.5 支持向量回归 SVR

  支持向量机除了可用于分类, 还可用于回归. 给定训练样本 $D = \{(\boldsymbol x_i, y_i)\}$, 考虑岭回归

$$\min _{\boldsymbol w, b} \frac 12 |\boldsymbol w| ^2 + C \sum _{i=1} ^m \ell (y_i - (\boldsymbol w ^T \boldsymbol x + b))$$

一般的最小二乘回归取损失函数 $\ell _z = z ^2$. 支持向量回归中的损失函数取 $\varepsilon$-不敏感损失:

$$\ell _\varepsilon (z) = \begin{cases} 0, \quad & |z| \leq \varepsilon, \\ |z| - \varepsilon, \quad & \text{otherwise} \end{cases}$$

即回归误差在 $\pm \varepsilon$ 以内时, 认为误差为零. 以外时, 按线性损失计. 引入松弛变量 $\hat{\boldsymbol \xi}, \boldsymbol \xi$, 问题可以重写为

$$\begin{aligned} \min _{\boldsymbol w, b, \hat{\boldsymbol \xi}, \boldsymbol \xi} \quad & \frac 12 |\boldsymbol w| ^2 + C \sum _{i=1} ^m (\xi _i + \hat \xi _i)\\ \text{s.t.} \quad & -(\varepsilon + \xi _i) \leq y_i - (\boldsymbol w ^T \boldsymbol x + b) \leq \varepsilon + \hat \xi _i\\ & \hat \xi _i \geq 0, \xi _i \geq 0, \forall i \end{aligned}$$

它的 Lagrange 函数是

$$\begin{aligned} & \mathcal L(\boldsymbol w, b, \boldsymbol \alpha, \hat{\boldsymbol \alpha}, \boldsymbol \xi, \hat{\boldsymbol \xi}, \boldsymbol \mu, \hat{\boldsymbol \mu})\\ & = \frac 12 |\boldsymbol w| ^2 + C \sum _{i=1} ^m (\xi _i + \hat \xi _i) - \sum _{i=1} ^m \mu _i \xi _i - \sum _{i=1} ^m \hat \mu _i \hat \xi _i\\ & + \sum _{i=1} ^m \alpha _i ((\boldsymbol w ^T \boldsymbol x + b) - y_i - \varepsilon - \xi _i) + \sum _{i=1} ^m \hat \alpha _i (y_i - (\boldsymbol w ^T \boldsymbol x + b) - \varepsilon - \hat \xi _i) \end{aligned}$$

其中 $\alpha _i \geq 0, \hat \alpha _i \geq 0, \mu _i \geq 0, \hat \mu _i \geq 0$ 是 Lagrange 乘子. 对 $\boldsymbol w, b, \boldsymbol \xi, \hat{\boldsymbol \xi}$ 求偏导并令其为零

$$\sum _{i=1}^m (\hat \alpha _i - \alpha _i) \boldsymbol x_i = \boldsymbol w, \quad \sum _{i=1}^m (\hat \alpha _i - \alpha _i) = \boldsymbol 0, \quad \boldsymbol \alpha + \boldsymbol \mu = \hat{\boldsymbol \alpha} + \hat{\boldsymbol \mu} = C \cdot \boldsymbol 1$$

它的对偶问题是

$$\begin{aligned} \max _{\boldsymbol \alpha, \hat{\boldsymbol \alpha}} \quad & \sum _{i=1}^m y_i (\hat \alpha _i - \alpha _i) - \varepsilon (\hat \alpha _i + \alpha _i)\\ & - \frac 12 \sum _{i=1}^m \sum _{j=1} ^m (\hat \alpha _i - \alpha _i) (\hat \alpha _j - \alpha _j) \boldsymbol x_i ^T \boldsymbol x_j\\ \text{s.t.} \quad & \sum _{i=1} ^m (\hat \alpha _i - \alpha _i) = 0, \\ & 0 \leq \alpha _i \leq C, 0 \leq \hat \alpha _i \leq C, \forall i \end{aligned}$$

它的 KKT 条件表明 $\alpha _i$ 和 $\hat \alpha _i$ 至少有一个为零. 两个都为零则说明样本落在 $\varepsilon$-间隔带内. 因为 $\boldsymbol w \sum (\hat \alpha _i - \alpha _i) \boldsymbol x_i$, 所以回归结果仅与间隔带以外的样本有关.

  若考虑核函数形式, 则相应的解为

$$\boldsymbol w = \sum _{i=1}^m (\hat \alpha _i - \alpha _i) \kappa(\boldsymbol x_i, \boldsymbol x)$$

其中 $\kappa(\cdot, \cdot)$ 是核函数.

6.6 核方法

  SVM 和 SVR 的结果总能表示成核函数 $\kappa(\boldsymbol x_i, \boldsymbol x)$ 的线性组合. 这一结论不是巧合, 因为有如下定理:

核函数表示定理 令 $|\cdot|$ 表示某种范数, 给定核函数 $\kappa(\cdot, \cdot)$, 在增函数 $\Omega(\cdot)$ 和损失函数 $\ell(\cdot)$ 下, 优化问题

$$\min _f \Omega(|h|) + \ell(f(\boldsymbol x_1), \cdot, f(\boldsymbol x_m))$$

的解总可以写成

$$f^*(\boldsymbol x) = \sum _{i=1}^m \alpha _i \kappa(\boldsymbol x_i, \boldsymbol x)$$

的形式.

  引入核函数称为核方法 (kernel methods) 可以将线性算法扩展到非线性. 以线性判别分析 LDA 为例, 尝试引入核线性判别分析 KLDA. 考虑一个映射 $\varphi : \mathcal X \to \mathcal F$ 将样本映射到特征空间 $\mathcal F$. 在 $\mathcal F$ 上求一条直线 $\boldsymbol w$, 使得点 $\boldsymbol x$ 在其上的投影

$$h(\boldsymbol x) = \boldsymbol w ^T \varphi(\boldsymbol x)$$

优化目标是

$$\max _{\boldsymbol w} \quad J(\boldsymbol w) := \frac{\boldsymbol w ^T S _{\rm b} \boldsymbol w}{\boldsymbol w ^T S _{\rm w} \boldsymbol w}$$

其中 $S_{\rm b}, S_{\rm w}$ 分别是样本映射到 $\boldsymbol F$ 后的类间散度矩阵和类内散度矩阵

$$S_{\rm b} := (\boldsymbol \mu _1 - \boldsymbol \mu _0)(\boldsymbol \mu _1 - \boldsymbol \mu _0) ^T, \quad S_{\rm w} := \sum _{i \in \mathbb B} \sum _{\boldsymbol x \in X_i} (\varphi(\boldsymbol x) - \mu _i)(\varphi(\boldsymbol x) - \mu _i) ^T$$

其中类均值 $\boldsymbol \mu _i := \sum _{\boldsymbol x \in X_i} \varphi(\boldsymbol x) / |X_i|$. 定义核函数 $\kappa(\boldsymbol x_i, \boldsymbol x) := \varphi(\boldsymbol x_i) ^T \varphi(\boldsymbol x)$.

  优化目标 $J(\boldsymbol w)$ 满足核函数表示定理的目标函数形式, 所以 $\exists \boldsymbol \alpha$ 使得

$$h^*(\boldsymbol x) = \sum _{i=1}^m \alpha _i \kappa(\boldsymbol x_i, \boldsymbol x) \quad \iff \quad \boldsymbol w^* = \sum _{i=1} ^m \alpha _i \varphi(\boldsymbol x_i)$$

  现在考虑求解 $\boldsymbol \alpha$. 定义 $K = (\kappa(\boldsymbol x_i, \boldsymbol x_j))_{m \times m}$ 是核矩阵. 令 $\boldsymbol 1_i \in \{0, 1\}^m$ 是第 $i$ 类样本的指示向量, $\boldsymbol 1_i$ 的第 $j$ 个分量为 $1$ 当且仅当 $\boldsymbol x_j \in X_i$, 否则为 $0$. 然后令

$$\hat{\boldsymbol \mu} _i := \frac{K \boldsymbol 1_i}{|X_i|}, \quad M := (\hat{\boldsymbol \mu} _1 - \hat{\boldsymbol \mu} _0)(\hat{\boldsymbol \mu} _1 - \hat{\boldsymbol \mu} _0) ^T, \quad N := K K^T - \sum _{i \in \mathbb B} |X_i| \hat{\boldsymbol \mu} _i \hat{\boldsymbol \mu} _i^T$$

此时优化目标变为

$$\max _{\boldsymbol \alpha} \quad J = \frac{\boldsymbol \alpha ^T M \boldsymbol \alpha}{\boldsymbol \alpha ^T N \boldsymbol \alpha}$$

这是 $M$ 与 $N$ 的广义 Rayleigh 商, 根据线性判别分析的求解方法求解即可.