《机器学习》笔记（第五部分：特征选择与稀疏学习、半监督学习、概率图模型）

11 特征选择与稀疏学习

11.1 子集搜索与评价

子集搜索 考虑子集搜索 (subset search) 问题:

• 前向 (forward) 搜索: 从空集开始, 每次添加一个属性, 直到模型最优;
• 后向 (backward) 搜索: 从全集开始, 每次删除一个属性, 直到模型最优;
• 双向 (bi-directional) 搜索: 从空集或全集开始, 每次考虑添加或删除一个属性, 直到模型最优.

子集评价 考虑子集评价 (subset evaluation) 问题: 给定数据集 $\boldsymbol D$, 假定 $y$ 类样本占比为 $p_y$. 定义信息熵

$$\mathop{\mathrm{Ent}} D = -\sum _y p_y \mathop{\mathrm{lb}} p_y$$

假定属性子集 $A$ 将 $D$ 做了一个不交的划分 $D = D_1 \cup \cdots \cup D_V$. 定义信息增益

$$\mathop{\mathrm{Gain}}_D A = \mathop{\mathrm{Ent}} D - \sum _v \frac{|D_v|}{|D|} \mathop{\mathrm{Ent}} D_v$$

信息增益 $\mathop{\mathrm{Gain}}_D A$ 越大, 意味着特征子集 $A$ 包含的信息越多. 可以以此作为评价准则.

  将子集搜索与子集评价结合, 就可以得到特征选择方法. 例如前向搜索与信息熵相结合就是决策树算法. 常见的特征选择方法包括过滤式 (filter)、包裹式 (wrapper) 和嵌入式 (embedding).

11.2 过滤式选择

  过滤式方法是最普通的特征选择方法: 先选择特征、再训练学习器, 特征选择与后续学习完全无关. Relief (Relevant Features), 是一种过滤式选择方法, 它给每一个特征评一个分 (称为相关统计量) 来度量其重要性.

  给定数据集 $D = \{(\boldsymbol x^{(i)}, y^{(i)})\}_{i=1}^{m}$, Relief 方法定义样本 $\boldsymbol x^{(i)}$ 的猜中近邻 (near-hit) $\boldsymbol u^{(i)}$ 和猜错近邻 $\boldsymbol v^{(i)}$ 分别为 $\boldsymbol x^{(i)}$ 的最近同类样本和异类样本. 然后定义关于第 $k$ 维的相关统计量

$$\delta _k = \sum _i \Big( - d(x^{(i)}_j, u^{(i)}_j)^2 + d(x^{(i)}_j, v^{(i)}_j)^2 \Big)$$

其中 $d(\cdot, \cdot)$ 是距离函数. 对于离散属性, 可取 0-1 距离; 对于离散属性, 可将 $\{x^{(i)}_j\}_i$ 规范化后取绝对值距离. 该分数分为两部分: 猜中近邻越远分数越低, 猜错近邻越远分数越高.

  Relief 是为二分类问题而设计的. 其扩展变体 Relief-F 用于处理多分类问题. 假设定义 $\boldsymbol x^{(i)}$ 类别为 $y$ 的最近邻为 $v^{(i)}(y)$, 则修正

$$\delta _k = \sum _i \Big( - d(x^{(i)}_j, u^{(i)}_j)^2 + \sum _{y \neq y_i} p(y) d(x^{(i)}_j, v^{(i)}_j(y))^2 \Big)$$

其中 $p_y$ 为类别 $y \in \mathcal Y$ 的频率.

11.3 包裹式选择

  包裹式选择直接把学习器性能作为特征子集的评价准则. LVW (Las Vegas Wreapper) 是一个典型的包裹式特征选择方法, 它在 Las Vegas 方法框架下使用随机策略来自己搜索, 以分类器误差作为特征子集的评价准则. 具体地, LVW 方法随机选取若干个特征子集, 计算每一个特征子集训练出的学习器的交叉验证误差, 然后选择误差率最低的那一个 (若误差率相等, 则特征数最少的那一个) 作为最终的分类器.

11.4 嵌入式选择、岭回归与 LASSO 回归

  嵌入选择将特征选择与学习器两个优化目标合为一个进行. 它同时考虑学习器是否合理以及特征选择是否合理, 故它的优化目标是两项的和. 简单线性回归中的优化目标是

$$\min _{\boldsymbol w} \sum _i (y_i - \boldsymbol w^T \boldsymbol x)^2$$

另外我们希望 $\boldsymbol w$ 的复杂程度尽量小. 这种复杂程度可以以某一个范数 $|\boldsymbol w|$ 刻画. 所以最终的优化目标是

$$\min _{\boldsymbol w} \quad \sum _i (y_i - \boldsymbol w^T \boldsymbol x)^2 + \lambda |\boldsymbol w|$$

其中 $\lambda > 0$ 是正则化系数. 若范数取 Euclid 范数, 则回归任务称为岭回归 (ridge regression); 若取 Manhattan 范数, 则称为 LASSO (Least Absolute Shrinkage and Selection Operator) 回归. 岭回归和 LASSO 回归都有助于降低过拟合风险, 其中岭回归更容易获得稀疏 (sprase) 解, 即 $\boldsymbol w$ 中的零分量会更多.

  LASSO 回归的求解可以使用近端梯度下降 (PGD, Proximal Gradient Descent) 解决. PGD 算法在每一个迭代步骤中将目标函数近似为一个二次函数, 然后求其最小值. 对于一个优化问题

$$\min _{\boldsymbol x} \quad f(\boldsymbol x) + \lambda ||\boldsymbol x||_1$$

若 $f$ 可导且 $\nabla f$ 满足 $L$-Lipschitz 条件, 即

$$\frac{||\nabla f(\boldsymbol x') - \nabla f(\boldsymbol x'')||_2^2}{||\boldsymbol x' - \boldsymbol x''||_2^2} \leq L, \quad \exists L > 0, \forall \boldsymbol x', \boldsymbol x''$$

选定一个初值 $\boldsymbol x_0$, 则优化目标可在 $\boldsymbol x_0$ 附近二阶 Taylor 展开成二次函数的形式. 这个函数形式的最小值点位于

$$\boldsymbol x_1 = \boldsymbol x_0 - \frac{\nabla f(\boldsymbol x_0)}{L}$$

首轮迭代最小值点 $\boldsymbol x_1$ 明确后, 又可以迭代地获得下一轮的最小值点, 如此反复直到收敛.

  在 LASSO 回归中, 我们选定一个初值 $\boldsymbol x_0$ 并计算首次迭代点 $\boldsymbol x_1 = \boldsymbol x_0 - \\nabla f(\boldsymbol x_0)/L$. 然后后续的所有迭代点都有解析解

$$x_{k+1, i} = \begin{cases} z_{ki} - \lambda / L, \quad & z_{ki} > \lambda / L\\ z_{ki} + \lambda / L, \quad & z_{ki} < -\lambda / L\\ 0, \quad & \text{Otherwise} \end{cases}$$

其中 $\boldsymbol z_k = (z_{k1}, \dots, z_{km}) = \boldsymbol x_k - \nabla f(\boldsymbol x_k) / L$.

11.5 稀疏表示与字典学习

  稀疏编码 (sparse coding) 问题考虑如何将样本矩阵稀疏化, 让其出现大量零值. 字典学习 (dictionary learning) 是稀疏编码的一种方法, 它尝试将样本 $D = \{\boldsymbol x_i \in \mathbb R^d\}_{i=1}^m$ 通过一个降维矩阵 (称为字典) $B \in \mathbb R^{d \times k}$ 降维到一个指定维数 $k$ (称为字典的词汇量) 的新表示 $\{\boldsymbol \alpha _i \in \mathbb R^k\}_{i=1}^m$, 并且希望新表示尽可能稀疏. 该问题与 LASSO 回归问题的目标函数形式一致, 但是决策变量不同:

$$\min _{B, \boldsymbol \alpha _i} \quad \sum _i \Big( ||\boldsymbol x_i - B \boldsymbol \alpha _i||_2^2 + \lambda ||\boldsymbol \alpha _i||_1 \Big)$$

其中 $B \boldsymbol \alpha _i$ 是基于投影 $\boldsymbol \alpha _i$ 复原的旧坐标. 该问题有 $kd + km$ 个决策变量, 难以求解.

  可以用变量交替优化的策略求解该问题. 第一步, 取一个随机的初值字典 $B$ 且固定住, 然后求解 LASSO 回归问题:

$$\boldsymbol \alpha _i \gets \argmin _{\boldsymbol \alpha _i} \sum _i \Big( ||\boldsymbol x_i - B \boldsymbol \alpha _i||_2^2 + \lambda ||\boldsymbol \alpha _i||_1 \Big)$$

得到一组 $\boldsymbol \alpha _i$ 后将其固定, 然后更新字典 $B$:

$$B \gets \argmin _B \sum _i \Big( ||\boldsymbol x_i - B \boldsymbol \alpha _i||_2^2 \Big)$$

该步骤可以使用基于逐列更新策略的 KSVD 方法求解. 重复上面两步, 直到收敛.

11.6 压缩感知

  假设对一个原始信号 $\boldsymbol x \in \mathbb R^m$ 用一个测量矩阵 $\Phi \in \mathbb R^{n \times m}$ 采样, 得到了一个采样信号 $\boldsymbol y = \Phi \boldsymbol x \in \mathbb R^n$ 且采样维度 $n \ll m$. 若只知道测量矩阵 $\Phi$ 和采样信号 $\boldsymbol y$, 当然是无法还原出原始信号 $\boldsymbol x$ 的. 但是如果原始信号 $\boldsymbol x$ 是由一个稀疏信号 $\boldsymbol s \in \mathrm R^m$ 通过一个线性变换 $\Phi \in \mathbb R^{m \times m}$ 产生的, 即 $\boldsymbol x = \Psi \boldsymbol s$, 则有

$$\boldsymbol y = \Phi \Psi \boldsymbol s =: A \boldsymbol s$$

由于 $\boldsymbol s$ 的稀疏性, 此时由采样信号 $\boldsymbol y$ 还原出稀疏信号 $\boldsymbol s$, 然后还原出原始信号 $\boldsymbol x = \Psi \boldsymbol s$ 是可能的.

  压缩感知分为感知测量和重构恢复两个阶段:

• 感知测量考虑如何将样本稀疏化, 方法包括 Fourier 变换、小波变换、字典学习、稀疏编码等;
• 重构恢复是压缩感知的核心, 关注如何将稀疏样本恢复成原信号.

限定等距性 对于一个降维矩阵 $A \in \mathbb R^{n \times m}\ (n \ll m)$ 若 $\exists \delta _k \in (0, 1)$ 使得 $\forall s \in \mathbb R^k$ 和 $\forall A_k \in \mathbb R^{n \times k}$ 是 $A$ 的子矩阵都有

$$1 - \delta _k \leq \frac{||A_k \boldsymbol s||_2^2}{||\boldsymbol s||_2^2} \leq 1 + \delta _k$$

则称 $A$ 满足 $k$-限定等距性 ($k$-RIP, Restricted Isometry Property).

  若 $A = \Phi \Psi$ 满足 $k$-限定等距性, 则可以从 $\boldsymbol y$ 中恢复出 $\boldsymbol s$, 从而还原 $\boldsymbol x$:

$$\min _{\boldsymbol s} \quad ||\boldsymbol s||_0, \qquad \text{s.t.} \quad \boldsymbol y = A \boldsymbol s$$

这本是一个 NP 难问题. 但是此处, $\mathrm L_0$ 范数优化与 $\mathrm L_1$ 范数优化是同解的. 所以该问题可以转化为一个优化目标为 $||\boldsymbol s||_1 = \min$ 的 LASSO 回归问题.

矩阵补全 假设一个矩阵 $A \in (\mathbb R \cup \{\varnothing\})^{n \times m} = (a_{ij})$ 有大量缺失值, 非缺失值的坐标记录在一个集合 $\Omega = \{(i, j)\}$ 中. 现在希望恢复一个低秩矩阵 $X = (x_{ij})$ 来对这些缺失值进行填补. 即

$$\min _X \quad \mathop{\mathrm{rank}} X, \qquad \text{s.t.} \quad x_{ij} = a_{ij}$$

这也是一个 NP 难问题. 定义矩阵 $X$ 的核范数 (nuclear norm) 或迹范数 (trace norm) $||X||_{\mathrm{nucl}}$ 是矩阵所有奇异值之和. 该问题的优化目标等价于 $||X||_{\mathrm{nucl}}$. 此时该问题可以通过半正定规划求解.

  理论研究表明, 通常只需观察到 $O(\mathop{\mathrm{rank} A \cdot m\log ^2m})$ 个元素就能完美恢复出 A.

13 半监督学习

13.1 未标记样本

  考虑一个样本集 $D = L \cup U$, 其中 $L = \{(\boldsymbol \ell _i, y_{\ell _i})\}_{i=1}^{n_\ell}$ 是有标记 (labeled) 样本, 而 $U = \{\boldsymbol u_i\}_{u=1}^{n_u}$ 是未标记 (unlabeled) 样本.

主动学习 用 $L$ 训练一个模型, 然后在 $U$ 中不断选出对改善模型性能帮助最大的样本并人工打标签 (称为查询, query). 该过程称为主动学习 (active learning).

半监督学习 $U$ 虽然未直接包含标记信息, 但包含了数据分布的信息, 对建立模型有帮助. 学习器不依赖外界、自动利用 $U$ 提升学习性能的过程称为半监督学习 (semi-supervised learning). 半监督学习分为两类:

• 纯 (pure) 半监督学习: 假定 $U$ 并非待预测数据. 基于开放世界假设, 希望模型适用于 $D$ 以外的数据.
• 直推学习 (transductive learining): 假定 $U$ 恰是待预测数据. 基于封闭世界假设, 仅试图对 $U$ 进行预测.

  利用 $U$ 必须要做出一些 $U$ 解释的数据分布信息与标记之间联系的假设. 常见的假设有:

• 聚类假设 (cluster assumption): 假设数据存在簇结构, 同簇样本属于同一类别.
• 流形假设 (manifold assumption): 假设数据分布在一个流形上, 邻近的样本具有相似的输出值.

13.2 生成式方法

  生成式方法 (generative methods) 假设所有数据都来源于同一个分布族, 此时模型参数与学习目标联系起来. 未标记数据的标记看作模型的缺失数据, 此时可以利用 EM 算法做极大似然估计.

  以 Gauss 混合分布为例, 给定样本 $\boldsymbol x$, 其真实类别标记为 $y \in \mathcal Y = \{1, \dots, N\}$. 假设样本服从 Gauss 混合分布:

$$\boldsymbol x \sim \mathrm{Mix}N(\boldsymbol \theta), \qquad \boldsymbol \theta = \{(\alpha _i, \boldsymbol \mu _i, \Sigma _i)\}_{i=1}^k$$

Gauss 混合分布的密度是

$$p(\boldsymbol x) = \sum _\iota \alpha _\iota \varphi(\boldsymbol x \mid \boldsymbol \mu _\iota, \Sigma _\iota)$$

定义样本 $\boldsymbol x$ 属于类别 $i$ 的概率:

$$p(\boldsymbol x, i) := \Pr(y = i \mid \boldsymbol x) = \frac{\alpha _i \varphi(\boldsymbol x \mid \boldsymbol \mu _i, \Sigma _i)}{p(\boldsymbol x)}$$

  这里采用 EM 算法求解参数的极大似然估计. 这里的观测数据是所有自变量 $\{\boldsymbol \ell _j\} \cup \{\boldsymbol u_j\}$ 以及有标签数据 $\boldsymbol \ell _j$ 属于类别 $i$ 的概率 $p_{i\ell _j} := \Pr(y_{\ell _j} = i) = \mathit 1(y_{\ell _j} = i)$. 缺失数据是无标签数据 $\boldsymbol u_j$ 属于类别 $i$ 的概率 $p_{iu_j} := \Pr(y_{u_j} = i)$. E-步考虑缺失数据的期望:

$$p_{iu_j} = p(\boldsymbol u_j, i)$$

这里 M-步考虑观测数据的对数似然最大化问题

$$LL = \sum _{(\boldsymbol x, y) \in L} \Big( p(\boldsymbol x) \cdot p(\boldsymbol x, i) \Big) + \sum _{\boldsymbol x \in U} p(\boldsymbol x) = \max$$

此时的参数为

$$\left\{ \begin{aligned} & \boldsymbol \mu _i = \frac{ \sum _j \boldsymbol \ell _j p_{i\ell _j} + \sum _j \boldsymbol u _j p_{iu _j} }{\sum _j p_{i\ell _j} + \sum _j p_{iu_j}}\\ & \Sigma _i = \frac{ \sum _j p_{i\ell _j} (\boldsymbol \ell _j - \boldsymbol \mu _i)(\boldsymbol \ell _j - \boldsymbol \mu _i)^T + \sum _j p_{iu _j} (\boldsymbol u _j - \boldsymbol \mu _i)(\boldsymbol u _j - \boldsymbol \mu _i)^T }{\sum _j p_{i\ell _j} + \sum _j p_{iu_j}}\\ & \alpha _i = \frac{\sum _j p_{i\ell _j} + \sum _j p_{iu_j}}{n_\ell + n_u} \end{aligned} \right.$$

以上过程不断迭代直到收敛, 即可获得模型参数. 对于新样本 $\boldsymbol x$, 尝试最大化后验概率 $\argmax _{i \in \mathcal Y} p(\boldsymbol x, i)$ 即可作为预测.

13.3 半监督支持向量机 S3VM

  半监督支持向量机 (S3VM, Semi-Supervised SVM) 是支持向量机在半监督学习上的推广. S3VM 试图找到一个能将两类样本分开, 并且穿过数据低密度区域的划分超平面.

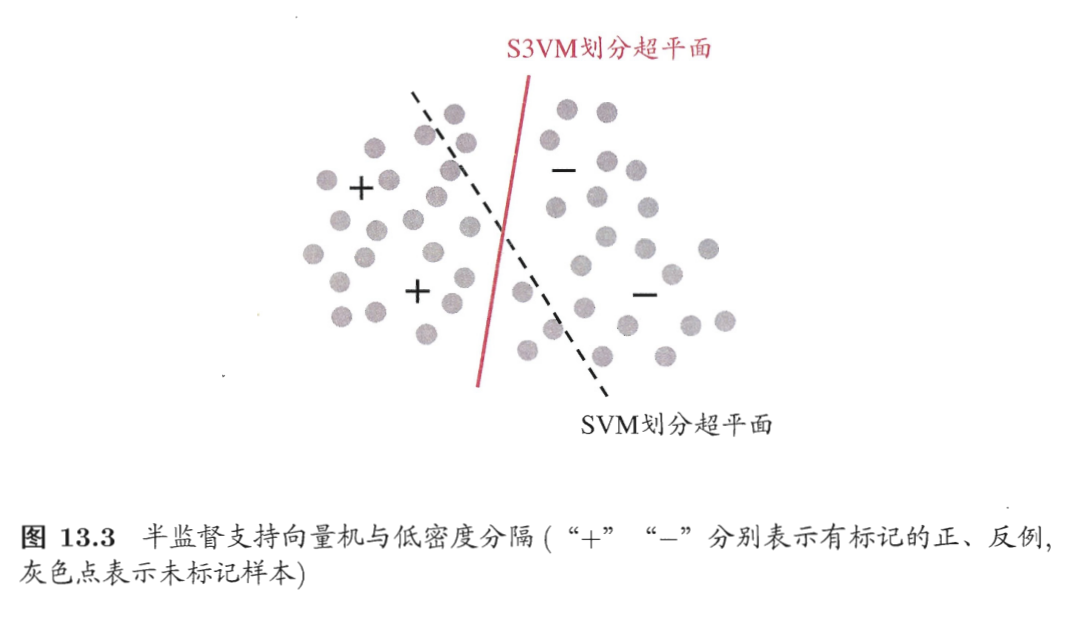
  TSVM (Transductive SVM) 是一种著名的 S3VM, 它尝试给 $U$ 中的样本指派一个最优类别. 给定样本 $L \cup U = \{(\boldsymbol \ell _i, y_{\ell _i})\}_{i=1}^{n_\ell} \cup \{(\boldsymbol u_i, y_{u_i})\}_{i=1}^{n_u}$, 其中 $y_{\ell _i}, y_{u_i} \in \mathbb B = \{\pm 1\}$. TSVM 尝试找到一组最优的分割超平面参数 $\boldsymbol w, b$、最优的松弛变量 $\xi _{\ell _i}, \xi _{u_i}$ 和最优的预测标记 $\hat y_{u_i}$, 使得

$$\begin{aligned} \min _{\boldsymbol w, b, \xi _{\ell _i}, \xi _{u_i}, \hat y_{u_i}} \quad & \frac 12 |\boldsymbol w| + C_L \sum \xi _{\ell _i} + C_U \sum \xi _{u_i}\\ \text{s.t.} \quad & \left\{ \begin{aligned} & y_{\ell _i} (\boldsymbol w^T \boldsymbol \ell _i + b) \geq 1 - \xi _{\ell _i}\\ & \hat y_{u_i} (\boldsymbol w^T \boldsymbol u_i + b) \geq 1 - \xi _{u_i}\\ & \xi _{\ell _i}, \xi _{u_i} \geq 0, \qquad \hat y_{u_i} \in \mathbb B \end{aligned} \right. \end{aligned}$$

这是一个 0-1 规划问题, 复杂度是 $\mathcal O(2^{n_u})$. 复杂度高主要是因为对 $U$ 样本类别的指派需要枚举. TSVM 采用局部搜索的策略寻找近似解, 要点如下:

1. 仅使用 $L$ 中的数据训练一个 SVM, 然后用其为 $U$ 做预测 (称为伪标记, pseudo-label) 进行标记指派 (label assignment).
2. 使用 $L$ 和指派后的 $U$ 训练一个 SVM. 注意此处初始化权重应该 $C_U \ll C_L$.
3. 考虑一对指派为异类, 且很可能分类出错的样本. 例如

$$\begin{aligned} (\ell _i, \ell _j) \quad \text{s.t.} \quad & \hat y_{\ell _i} = +1, \quad \hat y_{\ell _j} = -1,\\ & \xi _{\ell _i} > 0, \quad \xi _{\ell _j} > 0,\\ & \xi _{\ell _i} + \xi _{\ell _j} > 2 \end{aligned}$$

然后交换其指派类别, 再重新训练 SVM. 重复该过程, 直到找不到这样的样本对为止.

4. 增大权重 $C_U$, 例如 $C_U \gets \min(2C_U, C_L)$ 然后重新进行上一步 直到 $C_U = C_L$ 为止.

训练中可能会出现样本类别不平均的问题. 此时可将 $C_U$ 拆解为 $C_U^+$ 和 $C_U^-$ 两项, 分别对应 $U$ 中被指派的正反样本. 然后保持

$$C_U^+ \cdot |\{\hat y_{u_i} = +1\}| = C_U^- \cdot |\{\hat y_{u_i} = -1\}|$$

即可.

13.4 图半监督学习

13.4.1 二分类问题

  考虑标记传播 (label propagation) 方法. 给定一个数据集, 可将每个样本看成一个节点, 样本之间的边强度 (strength) 正比于样本之间的相关性. 将 $L$ 视为染色的样本, 现在要将颜色扩散至未染色的 $U$ 样本. 给定

$$L = \{(\boldsymbol x_i, y_i)\}_{i=1}^{n_\ell}, \quad U = \{(\boldsymbol x_i, y_i)\}_{i = n_\ell + 1}^{n_\ell + n_u}, \qquad n_\ell \ll n_u, \quad n_\ell + n_u = n$$

定义样本间距离为

$$d(\boldsymbol x_i, \boldsymbol x_j) = \exp -\frac{|\boldsymbol x_i - \boldsymbol x_j|^2}{2 \sigma ^2}$$

样本距离构成的矩阵 $W = (d(\boldsymbol x_i, \boldsymbol x_j))_{m \times m}$ 称为亲和矩阵 (affinity matrix). $\sigma > 0$ 是 Gauss 带宽 (构图参数).

  图半监督学习试图习得一个函数 $f: \mathcal X \to \mathbb R$, 使得分类规则 $y = \mathop{\mathrm{sgn}} f(\boldsymbol x) \in \mathbb B$. 我们希望相似的样本能被 $f$ 预测出相似的标记, 所以定义 $f$ 的能量函数 (energy function) 为

$$\begin{aligned} E(f) & = \frac 12 \sum _i \sum _j d(\boldsymbol x_i, \boldsymbol x_j) (f(\boldsymbol x_i) - f(\boldsymbol x_j))^2\\ & = \boldsymbol f^T (D - W) \boldsymbol f = \min \end{aligned}$$

这是一个二次型. 其中 $\boldsymbol f = (f(\boldsymbol x_1), \dots, f(\boldsymbol x_{n_\ell + n_u}))^T$ 是预测结果向量, $W = \mathop{\mathrm{diag} W\boldsymbol 1}$ 是亲和矩阵行和 (等价于列和) 向量生成的对角矩阵.

  现在求解最优的 $f$. 考虑分块矩阵

$$W = \begin{pmatrix} W_L & W_{UL}^T \\ W_{UL} & W_U \end{pmatrix}, \qquad D = \begin{pmatrix} D_L & O\\ O & D_U \end{pmatrix}, \qquad \boldsymbol f = \begin{pmatrix} \boldsymbol f_L\\ \boldsymbol f_U \end{pmatrix}$$

优化目标可重写为

$$E = \boldsymbol f_L^T (D_L - W_L) \boldsymbol f_L - 2 \boldsymbol f_U^T W_{UL} \boldsymbol f_L + \boldsymbol f_U^T (D_U - W_U) \boldsymbol f_U = \min$$

最优 $f$ 需要满足在 $L$ 上预测完全准确且在 $U$ 上有 $(D - W)\boldsymbol f = \boldsymbol 0$. 相较于考虑连续的 $f$, 我们只需考虑 $f$ 在 $U$ 上的预测值 (即 $\boldsymbol f_U$) 即可. 所以考虑 $\partial E / \partial \boldsymbol f_U = 0$ 可得

$$\boldsymbol f_U = (D_U - W_U) ^{-1} W_{UL} \boldsymbol f_L$$

为了简化上式, 考虑

$$\begin{aligned} P = D^{-1}W & = \begin{pmatrix} D_L^{-1} & O\\ O & D_U^{-1} \end{pmatrix} \begin{pmatrix} W_L & W_{UL}^T \\ W_{UL} & W_U \end{pmatrix}\\ & = \begin{pmatrix} D_L^{-1}W_L & D_L^{-1}W_{UL}^T\\ D_U^{-1}W_{UL} & D_U^{-1}W_U \end{pmatrix} =: \begin{pmatrix} P_U & *\\ P_{UL} & * \end{pmatrix} \end{aligned}$$

于是有

$$\boldsymbol f_U = (I - P_U)^{-1} P_{UL} \boldsymbol f_L$$

即最优解 $\boldsymbol f_U$ 是 $\boldsymbol f_L$ 的线性变换. 将 $L$ 中的标签 $(y_1, \dots, y_{n_\ell})$ 作为 $\boldsymbol f_L$ 代入即可得到 $U$ 的预测标签.

13.4.2 多分类问题

  考虑 $y_i \in \mathcal Y$ 是多分类标签. 考虑标记矩阵 $Y \in [0, 1]^{(n_\ell + n_u) \times |\mathcal Y|}$, 其中第 $i$ 行的 $|\mathcal Y|$ 个元素表示该样本属于每个类别的概率. 对于前 $n_\ell$ 行, 将其初始化为 $\mathit 1_{y_i = j}$, 对于后 $n_u$ 行全部置 $0$.

  初始化一个迭代矩阵 $F = Y$. 基于 $W$ 构造一个标记传播矩阵 $S = D^{-1/2} W D^{-1/2}$, 于是有迭代计算式

$$F \gets \alpha SF + (1-\alpha)Y$$

其中 $\alpha \in (0, 1)$ 是折中参数. 上面的迭代式收敛于

$$F^* = (1 - \alpha)(I - \alpha S)^{-1} Y$$

获得收敛的 $F^*$ 后, 检查其后 $n_u$ 行, 并取每一行值最大的类别作为 $U$ 标签的拟合结果.

13.5 基于分歧的方法

  基于分歧的方法 (disagreement-based methods) 使用多学习器产生标记, 而学习器之间的分歧 (disagreement) 对未标记数据的利用至关重要.

多视图数据 一个数据对象可能有多个属性集 (attribute set), 即 $\mathcal A = \{A^{(1)}, \dots, A^{({d})}\}$, 每一个属性集中包含若干属性 $A^{(i)} = \{a^{(i)}_1, \dots, a^{(i)}_{d_i}\}$. 一个属性集构成一个视图 (view), 则称该数据集为多视图 (multi-view) 数据. 记样本在属性集 $A^{(i)}$ 中各维度的取值为 $\boldsymbol x^{(i)}$, 则它有输出 $y^{(i)}$. 以 $d=2$ 为例, 该样本可以描述为 $\{(\boldsymbol x^{(1)}, y^{(1)}, \boldsymbol x^{(2)}, y^{(2)})\}$. 这是单个样本, 它有 $d_1 + d_2$ 个输入和 $2$ 个输出.

相容互补性 若各个属性集的输出是相同的, 即样本可以描述为 $(\boldsymbol x^{(1)}, \boldsymbol x^{(2)}, y)$ 的形式. 它有 $2$ 个输入和 $1$ 个输出, 则称不同视图具有相容性 (compatibility). 另一方面, 若基于 $A^{(1)}$ 和 $A^{(2)}$ 的学习器分别给出了相同的 $y$, 则有很大的把握认定 $y$ 是正确的. 即相容性基础上互补性会给学习器构建带来便利.

协同训练 协同训练 (co-training) 是基于分歧的方法的代表. 协同训练考虑 $2$ 个学习器, 每次互相将自身认为最有把握的无标签数据打上伪标签, 并作为对方下轮训练的有标签数据. 假设输入数据由相同标签的 $L^{(1)} = \{(\boldsymbol x^{(1)}_i, y_i)\}_i$ 和 $L^{(2)} = \{(\boldsymbol x^{(2)}_i, y_i)\}_i$ 构成, 则协同训练的算法要点如下:

1. 从 $U$ 中抽取样本进入缓冲池 $U_s$, 补满 $n_s$ 个样本.
2. 使用数据集 $L^{(1)}$ 训练学习器 $h^{(1)}$. 考察 $h^{(1)}$ 在 $U_s$ 样本上的分类置信度, 挑选 $n_p$ 个置信度最高的正例和 $n_n$ 个置信度最高的反例, 将其加入 $L^{(2)}$ 并从缓冲池 $U_s$ 删除.
3. 对数据集 $L^{(2)}$ 做同样的事情, 并且根据置信度更新 $L^{(1)}$.
4. 若 $h^{(1)}, h^{(2)}$ 无变化或迭代次数到达阈值, 则结束学习; 反之回到步骤 1.

  单视图数据可以使用协同训练的一些变体算法. 仅需弱学习器之间有显著的分歧, 即可通过相互提供伪标记样本的方式提高泛化性能.

13.6 半监督聚类

  虽然聚类是无监督学习任务, 但是如果对样本有额外监督信息, 则可加以利用获得更好聚类效果.

包含必连勿连信息的约束 $k$-均值算法 给定样本集合 $D = \{\boldsymbol x^{(i)}\}_{i=1}^m$, 监督信息包含以下两类:

• 必连 (must-link): 已知两个样本必属于同一簇, 记录必连约束集合 $\mathcal M = \{(\boldsymbol x^{(i)}, \boldsymbol x^{(j)})\}$.
• 勿连 (cannot-link): 已知两个样本必属于同一簇, 记录勿连约束集合 $\mathcal C = \{(\boldsymbol x^{(i)}, \boldsymbol x^{(j)})\}$.

半监督聚类考虑了约束 $k$-均值 (Constrained $k$-means) 算法, 该算法与一般的 $k$-均值算法唯一的区别在于, 计算样本与均值向量距离时应考虑最近的且不违背 $\mathcal M$ 和 $\mathcal C$ 约束的那一类.

包含少量有标记样本的约束种子 $k$-均值算法 假定一些已知类别的样本 $S_j \subseteq D$ 属于第 $j$ 类. 此时可以考虑约束种子 $k$-均值 (Constrained Seed $k$-means) 算法, 它与 $k$-均值算法唯一区别在于它初始化均值 $\boldsymbol \mu _j$ 为 $S_j$ 的重心, 并在开始时先将 $S_j$ 的所有样本直接标为第 $j$ 类.

14 概率图模型

  一个模型的变量分为三类: 所关心的变量 $Y$, 可观测的变量 $O$ 和其它变量 $R$. 概率模型 (probabilistic model) 将学习任务归结于计算变量的概率分布. 常见模型分为两类:

• 生成式 (generative) 模型, 考虑联合分布 $p(Y, R, O)$;
• 判别式 (discriminative) 模型, 考虑条件分布 $p(Y, R \mid O)$.

而推断 (inference) 根据生成式模型或判别式模型获得显式输出 $p(Y \mid O)$.

概率图模型 概率图模型 (probabilistic graphical model) 用一张图表达变量相关关系. 概率图模型分为两类:

• 用有向无环图表达变量间关系的有向图模型或 Bayes 网;
• 用无向图表达变量间关系的无向图模型或 Markov 网.

14.1 隐 Markov 模型 HMM

  隐 Markov 模型是一个时间序列模型, 它考虑一个无法观测的隐变量 (hidden variable) 时间序列随机变量 $\{y_t\}_{t=1}^n$, 取值于 $S = \{s_i\}_{i=1}^N$. 它又考虑一个可观测的观测变量时间序列随机变量 $\{x_t\}_{t=1}^n$, 取值于 $\Sigma = \{\sigma _i\}_{i=1}^N$. 隐 Markov 模型假设 $x_t$ 的值仅由 $y_t$ 决定, 且 $y_t$ 的值仅由 $y_{t-1}$ 决定.

  所以隐 Markov 模型是一个关于观测变量时间序列和隐变量时间序列 $(\boldsymbol x, \boldsymbol y) = (x_1, y_1, \dots, x_n, y_n)$ 的模型. 它有三个参数:

• 状态转移概率 $y_t$ 的值仅由 $y_{t-1}$ 决定. 定义 Markov 链的状态转移概率矩阵为

$$A = (a_{ij})_{N \times N}, \qquad a_{ij} = \Pr(y_t = s_j \mid y_{t-1} = s_i)$$

• 输出观测概率 $x_t$ 的值仅由 $y_t$ 决定. 定义观测变量的分布列, 以输出观测概率矩阵给出:

$$B = (b_{ij})_{N \times M}, \qquad b_{ij} = \Pr(x_t = \sigma _j \mid y_t = s_i)$$

• 初始状态概率 模型在初始时刻各状态出现的概率, 以向量形式给出:

$$\boldsymbol \pi = (\pi _1, \dots, \pi _N), \qquad \pi _i = \Pr(y_1 = s_i)$$

于是隐 Markov 模型可以表示为

$$(\boldsymbol x, \boldsymbol y) \sim \mathrm{HMM}(A, B, \boldsymbol \pi)$$

  在实际应用中, 人们关注隐 Markov 模型的三类问题:

• 给定参数 $(A, B, \boldsymbol \pi)$, 如何计算观测变量的分布列 $\Pr(\boldsymbol x = (\sigma _{i_1}, \dots, \sigma _{i_n}))$?
• 给定参数 $(A, B, \boldsymbol \pi)$ 和观测变量 $\boldsymbol x$, 如何计算最可能的隐变量 $\boldsymbol y$ 分布?
• 给定观测变量 $\boldsymbol x$, 如何计算最可能的参数 $(A, B, \boldsymbol \pi)$?

  基于 Markov 链的条件独立性假设

$$\Pr(y_t = s_i \mid y_{t-1}, y_{t-2}, y_1) = \Pr(y_t = s_i \mid y_{t-1})$$

隐 Markov 模型的这三个问题均能被高效求解.

14.2 Markov 随机场 MRF

  Markov 随机场 (MRF, Markov Random Field) 是典型的 Markov 网. 它是一个无向图, 节点之间的边表示变量间依赖关系.

团与极大团 图的全连接子集称为一个团 (clique). 平凡地, 任何相连的两个节点都构成一个团. 一个极大全连接子集称为一个极大团 (maximal clique).

势函数 设节点集为 $V$. 势函数 (potential functions) 或因子 (factor) 是定义在变量子集上的非负函数 $\psi: \mathbb R^{|Q|} \to \mathbb R^+_0$, 它用于定义概率分布. 考虑所有可能的团 $Q$ 构成的集合 $\mathcal C := \{Q\}$, 因为各个团之间概率相互独立, 所以样本的联合概率定义为

$$p(\boldsymbol x) \propto \prod _{Q \in \mathcal C} \psi _Q(\boldsymbol x_Q)$$

其中 $\psi _Q(\cdot)$ 是团 $Q$ 对应的势函数. 也可以仅考虑极大团 $Q^*$ 构成的集合 $\mathcal C^* := \{Q^*\}$, 则样本的联合概率定义为

$$p(\boldsymbol x) \propto \prod _{Q^* \in \mathcal C^*} \psi _Q^*(\boldsymbol x_{Q^*})$$

分离集 假设删除节点集 $C$ 后, 所有节点被分为 $A$ 和 $B$ 两个非联通节点集, 则称 $C$ 是一个分离集 (separating set).

全局 Markov 性 Markov 随机场有全局 Markov 性 (global Markov property): 对于被节点集 $C$ 分离的节点集 $A$ 和 $B$, 可以证明 $A$ 和 $B$ 在给定 $C$ 的条件下独立, 即

$$p(\boldsymbol x_A, \boldsymbol x_B \mid \boldsymbol x_C) = p(\boldsymbol x_A \mid \boldsymbol x_C) p(\boldsymbol x_B \mid \boldsymbol x_C)$$

记为 $\boldsymbol x_A \perp \boldsymbol x_B \mid \boldsymbol x_C$. 这是因为在 Markov 随机场中 $(A, C)$ 和 $(B, C)$ 分别是团, 所以其概率密度

$$\psi _{AC}(\boldsymbol x_A, \boldsymbol x_C) \psi _{BC}(\boldsymbol x_B, \boldsymbol x_C)$$

可以写成因子分解的形式.

  全局 Markov 性有两个重要推论:

• 局部 Markov 性 (local Markov property) 令 $a$ 是一个节点, $n(a)$ 是其邻接节点集 (即 $a$ 的 Markov 毯, Markov blanket), $V$ 是全集, 则

$$\boldsymbol x_a \perp \boldsymbol x_{V \setminus (\{a\} \cup n(a))} \mid \boldsymbol x_{n(a)}$$

• 成对 Markov 性 (pairwise Markov property) 令 $a, b$ 是一对非邻接节点, $V$ 是全集, 则

$$\boldsymbol x_a \perp \boldsymbol x_b \mid \boldsymbol x_{V \setminus \{a, b\}}$$

势函数的取值 势函数 $\psi: \mathbb R^{|Q|} \to \mathbb R^+_0$ 的作用是刻画变量相关关系, 它与变量概率分布成正比. 例如我们希望 $\boldsymbol x_A = \boldsymbol x_C$ 概率大, 则可以取

$$\psi _{AC}(\boldsymbol x_A, \boldsymbol x_C) = \begin{cases} 1.5, \quad & \boldsymbol x_A = \boldsymbol x_C\\ 0.1, \quad & \text{Otherwise} \end{cases}$$

为了满足非负性, 势函数可以通过一个普通实值函数做负指数变换得到

$$\psi _Q(\boldsymbol x_Q) = \exp -H_Q(\boldsymbol x_Q)$$

其中 $H_Q: \mathbb R^{|Q|} \to \mathbb R$ 是一个实值函数, 常见形式为

$$H_Q(\boldsymbol x_Q) = \sum _{u\neq v} \alpha _{uv} \boldsymbol x_u \boldsymbol x_v + \sum _u \beta _u \boldsymbol x_u$$

其中第一项考虑节点间关系, 第二项考虑单节点.

14.3 条件随机场 CRF

  令 $\boldsymbol x = \{x_i\}_{i=1}^n$ 是观测序列, $\boldsymbol y = \{y_i\}_{i=1}^n$ 是对应的标记序列. 标记序列可以是有无向图结构的, 例如自然语言处理中的线性数据 (词性标注) 和树形数据 (句子语法结构分析).

条件随机场 令节点集 $V$ 构成一个无向图. 对于节点 $v \in V$, 令 $y_v$ 表示 $v$ 对应的标记变量, $n(v)$ 表示 $v$ 的邻接节点集, 若 $\forall v \in V$ 都满足 Markov 性, 即

$$p(y_v \mid \boldsymbol x, \boldsymbol y_{V \setminus \{v\}}) = p(y_v \mid \boldsymbol x, \boldsymbol y_{n(v)})$$

则 $(\boldsymbol x, \boldsymbol y)$ 构成一个条件随机场 (CRF, Conditional Random Field).

链式条件随机场 链式条件随机场 (chain-structured CRF) 是 $\boldsymbol y$ 呈链式结构 $y_1 - y_2 - \cdots - y_n$ 的条件随机场. 可以定义势函数

$$p(\boldsymbol y \mid \boldsymbol x) \propto \exp \left( \sum _{i=1}^{n-1} t(y_i, y_{t+1}, x_i) + \sum _{i=1}^n s(y_i, x_i) \right)$$

其中 $t$ 是转移特征函数 (transition feature function), 刻画观测序列对相邻标记的影响; $s$ 是状态特征函数 (status feature function), 刻画观测序列对单个标记的影响. 例如状态特征函数

$$t(y_i, y_{t+1}, x_i) = \mathit 1( y_i = [V] \land y_{i+1} = [P] \land x_i = \text{``knock''} )$$

表示当当前词汇为 knock 时, 当前词汇很可能为动词. 再例如转移特征函数

$$t(y_{i+1}, y_i, x_i) = \mathit 1( y_i = [V] \land x_i = \text{``knock''} )$$

表示当当前词汇为 knock 时, 当前词汇很可能为动词, 下一个词汇很可能是介词. 势函数可以是转移特征函数和状态特征函数的线性组合的指数.

14.4 学习与推断

  假设图模型对应变量 $\boldsymbol x = \{x_i\}_{i=1}^n$ 能分为未知变量 $x_{i_0}$ 和已知变量集合 $\boldsymbol x_E = \{x_i\}_{i \neq i_0}$, 推断问题的目标就是计算条件概率

$$p(x_{i_0} \mid \boldsymbol x_E) = \frac{p(\boldsymbol x_E, x_{i_0})}{p(\boldsymbol x_E)} = \frac{p(\boldsymbol x_E, x_{i_0})}{\sum _{x_{i_0}} p(\boldsymbol x_E, x_{i_0})}$$

概率图模型解决了联合概率 $p(\boldsymbol x_E, x_{i_0})$ 的估计方法, 所以还需要考虑如何高效计算边际分布 $p(\boldsymbol x_E) = \sum _{x_{i_0}} p(\boldsymbol x_E, x_{i_0})$.

变量消去 以在有向结构 $x_1 \to x_2 \to x_3 \to x_4, \ x_3 \to x_5$ 计算 $p(x_5)$ 为例. 基于有向图模型描述的条件独立性, 有

$$p(x_5) = \sum _{x_1} \sum _{x_2} \sum _{x_3} \sum _{x_4} p(x_1) p(x_2 \mid x_1) p(x_3 \mid x_2) p(x_4 \mid x_3) p(x_4 \mid x_3)$$

可以按照 $(x_1, x_2, x_4, x_3)$ 的顺序步进地计算

$$p(x_5) = \sum _{x_3} \Bigg( p(x_5 \mid x_3) \sum _{x_4} p(x_4 \mid x_3) \sum _{x_2} \bigg( p(x_3 \mid x_2) \sum _{x_1} \Big( p(x_2 \mid x_1) p(x_1) \Big) \bigg) \Bigg)$$

这样就将一个四维求和问题转化为了四个一维求和问题.

  变量消去法中, 若要计算每个变量的边际分布的算法复杂度是 $\mathcal O(n^2)$, 这是因为很多中间量被重复使用了. 信念传播 (Belief Propagation) 是一种动态规划算法, 它将变量消去法中的中间量存储下来, 可以将算法复杂度降低到 $\mathcal O(n)$.

14.5 近似推断

  近似推断是推断的数值方法.

MCMC 采样 对于已知分布 $\boldsymbol X \sim p(\boldsymbol x)$ 的多元随机变量, 我们常常关注 $\boldsymbol X$ 的期望, 即

$$\mathrm E\boldsymbol X = \int _{x_1} \int _{x_2} \cdots \int _{x_n} \boldsymbol x p(\boldsymbol x) \mathrm dx_1 \mathrm dx_2 \cdots \mathrm dx_n$$

可以尝试构造出服从该分布的样本 $\{\boldsymbol x^{(k)}\}_{i=1}^N$, 然后求均值

$$\bar{\boldsymbol x} = \frac 1N \sum \boldsymbol x^{(k)}$$

作为期望的估计. Markov 链 Monte Carlo (MCMC, Markov Chain Monte Carlo) 方法设法构造一条平稳分布为 $p$ 的 Markov 链, 然后根据该 Markov 链迭代充分多次后的样本作为采样样本.

  Gibbs 采样方法是一种常见的 MCMC 方法. 它每次随机选取一个变量, 计算它的条件分布 $p(x_i \mid x_1, \dots, x_{i-1}, x_{i+1}, \dots, x_N)$ 并进行采样更新 $x_i$ 的值. 重复迭代, 每次生成一个样本.

14.6 话题模型

  话题模型 (topic model) 是一族生成式有向图模型, 可以用于自然语言处理. 隐 Dirichlet 分配模型 (LDA, Latent Dirichlet Allocation) 是话题模型的典型代表.

  假设词汇表中有 $N$ 种词汇, 有 $K$ 种话题, 第 $k$ 种话题中各种词汇的词频是 $\boldsymbol \beta _k \sim \mathrm{Dirichlet}_N (\boldsymbol \eta)$. 假设一篇文档 (document) 包含 $N$ 个词 $\{w_n\}_{n=1}^N$, 每个词根据以下步骤生成:

1. 生成文档的话题分布 $\boldsymbol \theta \sim \mathrm{Dirichlet}_K (\boldsymbol \alpha)$
2. 对于第 $n$ 个词, 先根据 $\boldsymbol \theta$ 选取话题 $z_n$, 再根据该话题对应的词频分布 $\boldsymbol \beta _k$ 随机采样生成词.

  以下考虑话题模型的概率密度. 该模型中的观测变量是文档内的词汇 $\boldsymbol w = \{w_n\}_{n=1}^N$; 隐变量包括每一个词所属的话题 $\boldsymbol z = \{z_n\}_{n=1}^N$、该文档的话题分布 $\boldsymbol \theta$ 和每个话题的词频分布 $\mathrm B = \{\boldsymbol \beta _k\}_{k=1}^K$; 参数包括话题内词频分布的 Dirichlet 参数 $\boldsymbol \alpha$. 所以整个模型的密度函数是

$$p(\boldsymbol w, \boldsymbol z, \mathrm B, \boldsymbol \theta \mid \boldsymbol \alpha, \boldsymbol \eta) = \sum _n p(w_n \mid z_n, \mathrm B) p(z_n \mid \boldsymbol \theta) \cdot p(\boldsymbol \theta \mid \boldsymbol \alpha) \cdot \sum _k p(\boldsymbol \beta _k \mid \boldsymbol \eta)$$

  一个常见的问题是给定数据集是一系列文档 $W = \{\boldsymbol w_i\}_{i=1}^T$, 求参数 $\boldsymbol \alpha$ 和 $\boldsymbol \eta$ 的估计. 考虑最大化对数似然

$$\ell(\boldsymbol \alpha, \boldsymbol \eta \mid W) = \sum _t \ln p(\boldsymbol w^{(t)} \mid \boldsymbol \alpha, \boldsymbol \eta) = \max$$

但 $p(\boldsymbol w^{(t)} \mid \boldsymbol \alpha, \boldsymbol \eta)$ 不易求解, 因此常使用变分法求近似解.

  另一个常见的问题是给定参数 $\boldsymbol \alpha$ 和 $\boldsymbol \eta$, 给定文档 $\boldsymbol w$, 推断文档对应的话题结构 (即隐变量 $\boldsymbol z$, $\boldsymbol \theta ^{(t)}$ 及 $\mathrm B^{(t)}$). 即求解

$$p(\boldsymbol z, \mathrm B, \boldsymbol \theta \mid \boldsymbol w, \boldsymbol \alpha, \boldsymbol \eta) = \frac{p(\boldsymbol w, \boldsymbol z, \mathrm B, \boldsymbol \theta \mid \boldsymbol \alpha, \boldsymbol \eta)}{p(\boldsymbol w \mid \boldsymbol \alpha, \boldsymbol \eta)}$$

该问题也经常使用 Gibbs 采样或者变分法求解.