《应用时间序列分析》笔记(第二部分:平稳序列建模)
4 平稳序列的拟合与预测
在用 ARMA 模型拟合数据前, 先要确保它是平稳非纯随机序列. 平稳性可以使用 ADF 单位根检验进行, 非纯随机性可以使用 Ljung-Box 检验进行.
4.2 单位根检验
单位根检验试图对所有特征根是否都在单位圆内进行检验, 从而检验序列是否平稳.
4.2.1 DF 单位根检验
给定时间序列 { x t } \{x_t\} { x t } A R M A ( 1 , q ) \mathrm{ARMA}(1, q) ARMA ( 1 , q )
X t = φ 1 X t − 1 + ξ t X_t = \varphi _1 X_{t-1} + \xi _t X t = φ 1 X t − 1 + ξ t 其中 ξ t ∼ N ( 0 , σ ξ 2 ) \xi _t \sim N(0, \sigma _\xi ^2) ξ t ∼ N ( 0 , σ ξ 2 ) λ = φ 1 ∈ ( − 1 , 1 ) \lambda = \varphi _1 \in (-1, 1) λ = φ 1 ∈ ( − 1 , 1 )
H 0 : ∣ φ 1 ∣ = 1 , H 1 : ∣ φ 1 ∣ < 1 H_0: |\varphi _1| = 1, \qquad
H_1: |\varphi _1| < 1 H 0 : ∣ φ 1 ∣ = 1 , H 1 : ∣ φ 1 ∣ < 1 基于样本对 φ 1 \varphi _1 φ 1
τ = ∣ φ ^ 1 ∣ − 1 s e ( φ ^ 1 ) \tau = \frac{|\hat \varphi _1| - 1}{\mathrm{se}(\hat \varphi _1)} τ = se ( φ ^ 1 ) ∣ φ ^ 1 ∣ − 1 虽然 DF 统计量是 t t t H 0 H_0 H 0 { X t } \{X_t\} { X t } t t t t t t
DF 检验的三种类型 DF 检验应用于三种常用模型. 根据原假设的结构不同, 拒绝域的临界值会不一样.
无漂移项自回归结构.
无延迟项模型 X t = ξ t X_t = \xi _t X t = ξ t
有延迟项模型 X t = φ 1 X t − 1 + ξ t X_t = \varphi _1 X_{t-1} + \xi _t X t = φ 1 X t − 1 + ξ t
若 DF 检验拒绝了上面某个结构的原假设, 说明在该结构下该时间序列 { X t } \{X_t\} { X t }
有漂移项自回归结构.
无延迟项模型 X t = φ 0 + ξ t X_t = \varphi _0 + \xi _t X t = φ 0 + ξ t
有延迟项模型 X t = φ 0 + φ 1 X t − 1 + ξ t X_t = \varphi _0 + \varphi _1 X_{t-1} + \xi _t X t = φ 0 + φ 1 X t − 1 + ξ t
若 DF 检验拒绝了上面某个结构的原假设, 说明在该结构下该时间序列 { X t } \{X_t\} { X t }
关于时间 t t t
无延迟项模型 X t = α + β t + ξ t X_t = \alpha + \beta t + \xi _t X t = α + βt + ξ t
有延迟项模型 X t = α + β t + φ 1 X t − 1 + ξ t X_t = \alpha + \beta t + \varphi _1 X_{t-1} + \xi _t X t = α + βt + φ 1 X t − 1 + ξ t
若 DF 检验拒绝了上面某个结构的原假设, 说明在该结构下该时间序列的趋势可以用线性模型提取, 提取后的残差项 { ξ t } \{\xi _t\} { ξ t }
4.2.2 ADF 单位根检验
DF 检验只考虑 A R ( 1 ) \mathrm{AR}(1) AR ( 1 ) A R ( p ) \mathrm{AR}(p) AR ( p ) A R ( p ) \mathrm{AR}(p) AR ( p )
λ p − φ 1 λ p − 1 − ⋯ − φ p = 0 \lambda ^p - \varphi _1 \lambda ^{p-1} - \cdots - \varphi _p = 0 λ p − φ 1 λ p − 1 − ⋯ − φ p = 0 若有单位根存在, 即 λ = 1 \lambda = 1 λ = 1 φ 1 + ⋯ + φ p = 1 \varphi _1 + \cdots + \varphi _p = 1 φ 1 + ⋯ + φ p = 1
H 0 : φ 1 + ⋯ + φ p = 1 , H 1 : φ 1 + ⋯ + φ p < 1 H_0: \varphi _1 + \cdots + \varphi _p = 1, \qquad
H_1: \varphi _1 + \cdots + \varphi _p < 1 H 0 : φ 1 + ⋯ + φ p = 1 , H 1 : φ 1 + ⋯ + φ p < 1 计算 ADF 统计量
τ = ∑ φ ^ i − 1 s e ( ∑ φ ^ i ) \tau = \frac{\sum \hat \varphi _i - 1}{\mathrm{se}(\sum \hat \varphi _i)} τ = se ( ∑ φ ^ i ) ∑ φ ^ i − 1 ADF 统计量也服从一个与 t t t
ADF 检验的三种类型 ADF 检验也可以应用于三种常用模型.
无漂移项自回归结构.
有 p p p X t = φ 1 X t − 1 + ⋯ + φ p X t − p + ξ t X_t = \varphi _1 X_{t-1} + \cdots + \varphi _p X_{t-p} + \xi _t X t = φ 1 X t − 1 + ⋯ + φ p X t − p + ξ t
有漂移项自回归结构.
有 p p p X t = φ 0 + φ 1 X t − 1 + ⋯ + φ p X t − p + ξ t X_t = \varphi _0 + \varphi _1 X_{t-1} + \cdots + \varphi _p X_{t-p} + \xi _t X t = φ 0 + φ 1 X t − 1 + ⋯ + φ p X t − p + ξ t
关于时间 t t t
有 p p p X t = α + β t + φ 1 X t − 1 + ⋯ + φ p X t − p + ξ t X_t = \alpha + \beta t + \varphi _1 X_{t-1} + \cdots + \varphi _p X_{t-p} + \xi _t X t = α + βt + φ 1 X t − 1 + ⋯ + φ p X t − p + ξ t
4.3 模型识别
样本 ACF 定义为
ρ ^ k = ∑ t = 1 n − k ( x t − x ˉ ) ( x t + k − x ˉ ) ∑ t = 1 n ( x t − x ˉ ) 2 \hat \rho _k = \frac{\sum _{t=1}^{n-k}(x_t - \bar x)(x_{t+k} - \bar x)}{\sum _{t=1}^n (x_t - \bar x)^2} ρ ^ k = ∑ t = 1 n ( x t − x ˉ ) 2 ∑ t = 1 n − k ( x t − x ˉ ) ( x t + k − x ˉ ) 它是一个有偏估计
E ρ ^ k = ( 1 − k n ) ρ k E\hat \rho _k = \left(1 - \frac kn\right) \rho _k E ρ ^ k = ( 1 − n k ) ρ k 样本 PACF 定义为
φ ^ k k = ∣ 1 ρ ^ 1 ⋯ ρ ^ 1 ρ ^ 1 1 ⋯ ρ ^ 2 ⋮ ⋮ ⋱ ⋮ ρ ^ k − 1 ρ ^ k − 2 ⋯ ρ ^ k ∣ / ∣ 1 ρ ^ 1 ⋯ ρ ^ k − 1 ρ ^ 1 1 ⋯ ρ ^ k − 2 ⋮ ⋮ ⋱ ⋮ ρ ^ k − 1 ρ ^ k − 2 ⋯ 1 ∣ \hat \varphi _{kk} =
\begin{vmatrix}
1 & \hat \rho _1 & \cdots & \hat \rho _1\\
\hat \rho _1 & 1 & \cdots & \hat \rho _2\\
\vdots & \vdots & \ddots & \vdots\\
\hat \rho _{k-1} & \hat \rho _{k-2} & \cdots & \hat \rho _k
\end{vmatrix} \Bigg/
\begin{vmatrix}
1 & \hat \rho _1 & \cdots & \hat \rho _{k-1}\\
\hat \rho _1 & 1 & \cdots & \hat \rho _{k-2}\\
\vdots & \vdots & \ddots & \vdots\\
\hat \rho _{k-1} & \hat \rho _{k-2} & \cdots & 1
\end{vmatrix} φ ^ kk = 1 ρ ^ 1 ⋮ ρ ^ k − 1 ρ ^ 1 1 ⋮ ρ ^ k − 2 ⋯ ⋯ ⋱ ⋯ ρ ^ 1 ρ ^ 2 ⋮ ρ ^ k / 1 ρ ^ 1 ⋮ ρ ^ k − 1 ρ ^ 1 1 ⋮ ρ ^ k − 2 ⋯ ⋯ ⋱ ⋯ ρ ^ k − 1 ρ ^ k − 2 ⋮ 1 它们都渐进服从正态分布
ρ ^ k ∼ ˙ N ( 0 , 1 / n ) , φ ^ k k ∼ ˙ N ( 0 , 1 / n ) \hat \rho _k \mathop{\dot \sim} N(0, 1/n), \qquad
\hat \varphi _{kk} \mathop{\dot \sim} N(0, 1/n) ρ ^ k ∼ ˙ N ( 0 , 1/ n ) , φ ^ kk ∼ ˙ N ( 0 , 1/ n ) 故可以使用 2 σ 2\sigma 2 σ
考虑样本 ACF 图和 PACF 图. 先看 ACF 和 PACF 分别是拖尾 (即其绝对值呈指数衰减) 还是截尾, 来定用 AR、MA 还是 ARMA 模型拟合; 若使用 AR 或 MA 模型, 则再看 ACF 或 PACF 的截尾阶数, 来确定 p p p q q q
若 ACF 拖尾、PACF p p p A R ( p ) \mathrm{AR}(p) AR ( p )
若 ACF q q q M A ( q ) \mathrm{MA}(q) MA ( q )
若 ACF 和 PACF 都拖尾, 则识别为 A R M A ( p , q ) \mathrm{ARMA}(p, q) ARMA ( p , q )
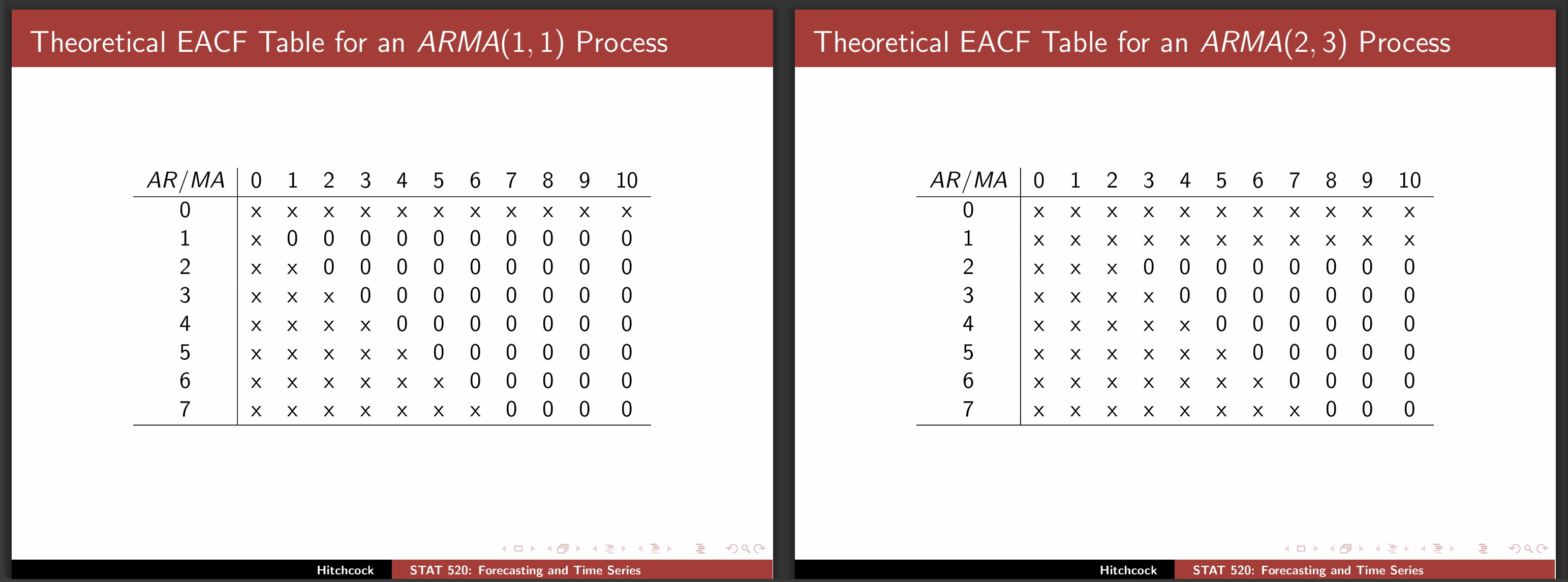
ARMA 模型的一种定阶方法是使用三角格子法. 给定一个平稳非纯随机时间序列数据 { X t } \{X_t\} { X t } ( i , j ) (i, j) ( i , j )
考虑 A R ( i ) \mathrm{AR}(i) AR ( i ) ( X t − 1 , … , X t − i ) (X_{t-1}, \dots, X_{t-i}) ( X t − 1 , … , X t − i ) X t X_t X t ( φ ~ 1 , … , φ ~ i ) (\tilde \varphi _1, \dots, \tilde \varphi _i) ( φ ~ 1 , … , φ ~ i )
定义消除 AR 部分后的新序列 W t = X t − φ ~ i X t − 1 − ⋯ − φ ~ i X t − i W_t = X_t - \tilde \varphi _i X_{t-1} - \cdots - \tilde \varphi _i X_{t-i} W t = X t − φ ~ i X t − 1 − ⋯ − φ ~ i X t − i M A ( j ) \mathrm{MA}(j) MA ( j )
{ X t } \{X_t\} { X t } ( i , j ) (i, j) ( i , j ) { W t } \{W_t\} { W t } j j j
然后绘制 EACF 表, 将显著不为零的 EACF 用叉号显示, 否则用 0 0 0
注 ACF 图和 PACF 图的特征, 可以帮助我们进行 ARMA 模型的阶数识别, 但显然图识别具有很大的主观性, 这可能会使部分研究人员产生焦虑, 担心自己识别错误造成严重的系统性错误. 其实不必太担心这个问题, 因为平稳可逆的 ARMA 模型存在整体自洽性, 即 AR 模型可以转化为 MA 模型, MA 模型也可以转化为 AR 模型. 因此, 对于 ARMA 模型的阶数识别并没有唯一结果. 很可能出现同一个序列, 使用不同的阶数识别, 都能得到不错的拟合效果.
4.4 参数估计
A R M A ( p , q ) \mathrm{ARMA}(p, q) ARMA ( p , q )
X t = φ 0 + φ 1 X t − 1 + ⋯ + φ p X t − p + ε t − θ 1 ε t − 1 − ⋯ − θ q ε t − q X_t = \varphi _0 + \varphi _1 X_{t-1} + \cdots + \varphi _p X_{t-p} + \varepsilon _t - \theta _1 \varepsilon _{t-1} - \cdots - \theta _q \varepsilon _{t-q} X t = φ 0 + φ 1 X t − 1 + ⋯ + φ p X t − p + ε t − θ 1 ε t − 1 − ⋯ − θ q ε t − q 其中 ε t ∼ W N ( 0 , σ ε 2 ) \varepsilon _t \sim WN(0, \sigma _\varepsilon ^2) ε t ∼ W N ( 0 , σ ε 2 ) p + q + 2 p+q+2 p + q + 2
φ 0 , ( φ 1 , … , φ p ) , ( θ 1 , … , θ q ) , σ ε 2 \varphi _0, (\varphi _1, \dots, \varphi _p), (\theta _1, \dots, \theta _q), \sigma _\varepsilon ^2 φ 0 , ( φ 1 , … , φ p ) , ( θ 1 , … , θ q ) , σ ε 2 总体均值一般使用样本均值估计
φ ^ 0 = x ˉ = 1 n ∑ x i \hat \varphi _0 = \bar x = \frac 1n \sum x_i φ ^ 0 = x ˉ = n 1 ∑ x i 在中心化 x t ← x t − x ˉ x_t \gets x_t - \bar x x t ← x t − x ˉ φ 0 \varphi _0 φ 0 p + q + 1 p+q+1 p + q + 1
4.4.1 矩估计
首先考虑系数 ( φ 1 , … , φ p ) , ( θ 1 , … , θ q ) (\varphi _1, \dots, \varphi _p), (\theta _1, \dots, \theta _q) ( φ 1 , … , φ p ) , ( θ 1 , … , θ q ) ρ i = ρ i ( φ 1 , … , φ p , θ 1 , … , θ q ) \rho _i = \rho _i(\varphi _1, \dots, \varphi _p, \theta _1, \dots, \theta _q) ρ i = ρ i ( φ 1 , … , φ p , θ 1 , … , θ q ) p + q p+q p + q
ρ 1 = ρ ^ 1 , … , ρ p + 1 = ρ ^ p + q \rho _1 = \hat \rho _1, \quad
\dots, \quad
\rho _{p+1} = \hat \rho _{p+q} ρ 1 = ρ ^ 1 , … , ρ p + 1 = ρ ^ p + q 就可以解得参数的矩估计 ( φ ^ 1 , … , φ ^ p ) , ( θ ^ 1 , … , θ ^ q ) (\hat \varphi _1, \dots, \hat \varphi _p), (\hat \theta _1, \dots, \hat \theta _q) ( φ ^ 1 , … , φ ^ p ) , ( θ ^ 1 , … , θ ^ q )
再考虑白噪声方差 σ ε 2 \sigma _\varepsilon ^2 σ ε 2 x ˉ 1 , … , x ˉ n \bar x_1, \dots, \bar x_n x ˉ 1 , … , x ˉ n
σ ^ ε 2 = 1 n ∑ ( x i − x ^ i ) 2 \hat \sigma _\varepsilon ^2 = \frac 1n \sum (x_i - \hat x_i)^2 σ ^ ε 2 = n 1 ∑ ( x i − x ^ i ) 2
例 计算 A R ( 2 ) \mathrm{AR}(2) AR ( 2 )
ρ 1 = φ 1 1 − φ 2 , ρ 2 = φ 1 2 1 − φ 2 + φ 2 \rho _1 = \frac{\varphi _1}{1 - \varphi _2}, \qquad
\rho _2 = \frac{\varphi _1^2}{1 - \varphi _2} + \varphi _2 ρ 1 = 1 − φ 2 φ 1 , ρ 2 = 1 − φ 2 φ 1 2 + φ 2 联立
ρ 1 = ρ ^ 1 , ρ 2 = ρ ^ 2 \rho _1 = \hat \rho _1, \quad
\rho _2 = \hat \rho _2 ρ 1 = ρ ^ 1 , ρ 2 = ρ ^ 2 可得矩估计
φ ^ 1 = 1 − ρ ^ 2 1 − ρ ^ 2 ρ 1 , φ ^ 2 = ρ 2 − ρ 1 2 1 − ρ 1 2 \hat \varphi _1 = \frac{1 - \hat \rho _2}{1 - \hat \rho ^2} \rho _1, \quad
\hat \varphi _2 = \frac{\rho _2 - \rho _1^2}{1 - \rho _1^2} φ ^ 1 = 1 − ρ ^ 2 1 − ρ ^ 2 ρ 1 , φ ^ 2 = 1 − ρ 1 2 ρ 2 − ρ 1 2
实际上对于 A R ( p ) \mathrm{AR}(p) AR ( p )
( 1 ρ 1 ⋯ ρ k − 1 ρ 1 1 ⋯ ρ k − 2 ⋮ ⋮ ⋱ ⋮ ρ k − 1 ρ k − 2 ⋯ 1 ) ( φ ^ 1 φ ^ 2 ⋮ φ ^ k ) = ( ρ 1 ρ 2 ⋮ ρ k ) \begin{pmatrix}
1 & \rho _1 & \cdots & \rho _{k-1}\\
\rho _1 & 1 & \cdots & \rho _{k-2}\\
\vdots & \vdots & \ddots & \vdots\\
\rho _{k-1} & \rho _{k-2} & \cdots & 1
\end{pmatrix}
\begin{pmatrix}
\hat \varphi _1\\
\hat \varphi _2\\
\vdots\\
\hat \varphi _k
\end{pmatrix} =
\begin{pmatrix}
\rho _1\\
\rho _2\\
\vdots\\
\rho _k
\end{pmatrix} 1 ρ 1 ⋮ ρ k − 1 ρ 1 1 ⋮ ρ k − 2 ⋯ ⋯ ⋱ ⋯ ρ k − 1 ρ k − 2 ⋮ 1 φ ^ 1 φ ^ 2 ⋮ φ ^ k = ρ 1 ρ 2 ⋮ ρ k 考虑 Cramer 法则可以得到矩估计的显式解
φ ^ i = ∣ 1 ρ 1 ⋯ ρ 1 ⋯ ρ k − 1 ρ 1 1 ⋯ ρ 2 ⋯ ρ k − 2 ⋮ ⋮ ⋮ ⋮ ρ k − 1 ρ k − 2 ⋯ ρ k ⋯ 1 ∣ / ∣ 1 ρ 1 ⋯ ρ k − 1 ρ 1 1 ⋯ ρ k − 2 ⋮ ⋮ ⋱ ⋮ ρ k − 1 ρ k − 2 ⋯ 1 ∣ \hat \varphi _i =
\begin{vmatrix}
1 & \rho _1 & \cdots & \rho _1 & \cdots & \rho _{k-1}\\
\rho _1 & 1 & \cdots & \rho _2 & \cdots & \rho _{k-2}\\
\vdots & \vdots & & \vdots & & \vdots\\
\rho _{k-1} & \rho _{k-2} & \cdots & \rho _k & \cdots & 1
\end{vmatrix} \Bigg/
\begin{vmatrix}
1 & \rho _1 & \cdots & \rho _{k-1}\\
\rho _1 & 1 & \cdots & \rho _{k-2}\\
\vdots & \vdots & \ddots & \vdots\\
\rho _{k-1} & \rho _{k-2} & \cdots & 1
\end{vmatrix} φ ^ i = 1 ρ 1 ⋮ ρ k − 1 ρ 1 1 ⋮ ρ k − 2 ⋯ ⋯ ⋯ ρ 1 ρ 2 ⋮ ρ k ⋯ ⋯ ⋯ ρ k − 1 ρ k − 2 ⋮ 1 / 1 ρ 1 ⋮ ρ k − 1 ρ 1 1 ⋮ ρ k − 2 ⋯ ⋯ ⋱ ⋯ ρ k − 1 ρ k − 2 ⋮ 1
例 计算 M A ( 1 ) \mathrm{MA}(1) MA ( 1 ) ρ 1 = − θ 1 / ( 1 + θ 1 2 ) \rho _1 = -\theta _1 / (1 + \theta _1^2) ρ 1 = − θ 1 / ( 1 + θ 1 2 ) ρ 1 = ρ ^ 1 \rho _1 = \hat \rho _1 ρ 1 = ρ ^ 1
θ ^ 1 = − 1 + 1 − 4 ρ ^ 1 2 2 ρ ^ 1 \hat \theta _1 = \frac{-1 + \sqrt{1 - 4 \hat \rho _1^2}}{2 \hat \rho _1} θ ^ 1 = 2 ρ ^ 1 − 1 + 1 − 4 ρ ^ 1 2 另一个根被舍弃了, 因为 M A ( 1 ) \mathrm{MA}(1) MA ( 1 ) ∣ θ 1 ∣ < 1 |\theta _1| < 1 ∣ θ 1 ∣ < 1
例 计算 A R M A ( 1 , 1 ) \mathrm{ARMA}(1, 1) ARMA ( 1 , 1 )
ρ 1 = γ k σ 2 = ( φ 1 − θ 1 ) ( 1 − φ 1 θ 1 ) 1 + θ 1 2 − 2 φ 1 θ 1 , ρ 2 = φ 1 ρ 1 \rho _1 = \frac{\gamma _k}{\sigma ^2} = \frac{(\varphi _1 - \theta _1) (1 - \varphi _1 \theta _1)}{1 + \theta _1^2 - 2\varphi _1 \theta _1}, \qquad
\rho _2 = \varphi _1 \rho _1 ρ 1 = σ 2 γ k = 1 + θ 1 2 − 2 φ 1 θ 1 ( φ 1 − θ 1 ) ( 1 − φ 1 θ 1 ) , ρ 2 = φ 1 ρ 1 考虑可逆条件且经过复杂的计算可以得到矩估计的唯一解
φ ^ 1 = ρ ^ 2 ρ ^ 1 , θ ^ 1 = { ( c + c 2 − 4 ) / 2 , c ≤ − 2 ( c − c 2 − 4 ) / 2 , c ≥ 2 , c = 1 − φ ^ 1 2 − 2 ρ ^ 2 φ ^ 1 − ρ ^ 1 \hat \varphi _1 = \frac{\hat \rho _2}{\hat \rho _1}, \quad
\hat \theta _1 = \begin{cases}
(c + \sqrt{c^2 - 4}) / 2, & c \leq -2\\
(c - \sqrt{c^2 - 4}) / 2, & c \geq 2
\end{cases}, \quad
c = \frac{1 - \hat \varphi _1 ^2 - 2 \hat \rho 2}{\hat \varphi _1 - \hat \rho _1} φ ^ 1 = ρ ^ 1 ρ ^ 2 , θ ^ 1 = { ( c + c 2 − 4 ) /2 , ( c − c 2 − 4 ) /2 , c ≤ − 2 c ≥ 2 , c = φ ^ 1 − ρ ^ 1 1 − φ ^ 1 2 − 2 ρ ^ 2
矩估计计算量小, 简单直观, 不需要假设总体分布; 但仅用到了样本二阶矩的信息, 比较粗糙, 估计精度不高, 因此仅常用于确定极大似然估计和最小二乘估计的迭代初值.
4.4.2 极大似然估计
在极大似然估计中, 我们假设中心化样本 x = ( x 1 , … , x n ) T \boldsymbol x = (x_1, \dots, x_n)^T x = ( x 1 , … , x n ) T β = ( φ 1 , … , φ p , θ 1 , … , θ q ) T \boldsymbol \beta = (\varphi _1, \dots, \varphi _p, \theta _1, \dots, \theta _q)^T β = ( φ 1 , … , φ p , θ 1 , … , θ q ) T
γ k = ( ∑ i = 0 ∞ G i G i + k ) σ ε 2 \gamma _k = \left(\sum_{i=0}^\infty G_{i}G_{i+k}\right) \sigma _\varepsilon ^2 γ k = ( i = 0 ∑ ∞ G i G i + k ) σ ε 2 它是参数 β \boldsymbol \beta β x \boldsymbol x x
x ∼ N ( 0 , Ω σ ε 2 ) , Ω = ( ∑ i = 0 ∞ G i 2 ⋯ ∑ i = 0 ∞ G i G i + n − 1 ⋮ ⋱ ⋮ ∑ i = 0 ∞ G i G i + n − 1 ⋯ ∑ i = 0 ∞ G i 2 ) \boldsymbol x \sim N(\boldsymbol 0, \Omega \sigma _\varepsilon ^2), \qquad
\Omega = \begin{pmatrix}
\sum\limits_{i=0}^\infty G_i^2 & \cdots & \sum\limits_{i=0}^\infty G_iG_{i+n-1}\\
\vdots & \ddots & \vdots\\
\sum\limits_{i=0}^\infty G_iG_{i+n-1} & \cdots & \sum\limits_{i=0}^\infty G_i^2
\end{pmatrix} x ∼ N ( 0 , Ω σ ε 2 ) , Ω = i = 0 ∑ ∞ G i 2 ⋮ i = 0 ∑ ∞ G i G i + n − 1 ⋯ ⋱ ⋯ i = 0 ∑ ∞ G i G i + n − 1 ⋮ i = 0 ∑ ∞ G i 2 样本的似然函数是多元正态分布的密度函数
L ( β ∣ x ) = 1 ( 2 π σ ε 2 ) k ∣ Ω ∣ exp − x T Ω − 1 x 2 σ ε 2 \mathcal L(\boldsymbol \beta \mid \boldsymbol x) = \frac{1}{\sqrt{(2 \pi \sigma _\varepsilon ^2)^k |\Omega|}} \exp -\frac{\boldsymbol x^T \Omega ^{-1} \boldsymbol x}{2 \sigma _\varepsilon ^2} L ( β ∣ x ) = ( 2 π σ ε 2 ) k ∣Ω∣ 1 exp − 2 σ ε 2 x T Ω − 1 x 它的对数似然函数是
ℓ ( β ∣ x ) = − n 2 ln 2 π − n 2 ln σ ε 2 − 1 2 ln ∣ Ω ∣ − x T Ω − 1 x 2 σ ε 2 \ell(\boldsymbol \beta \mid \boldsymbol x) = -\frac n2 \ln 2\pi - \frac n2 \ln \sigma _\varepsilon ^2 - \frac 12 \ln |\Omega| - \frac{\boldsymbol x^T \Omega ^{-1} \boldsymbol x}{2 \sigma _\varepsilon ^2} ℓ ( β ∣ x ) = − 2 n ln 2 π − 2 n ln σ ε 2 − 2 1 ln ∣Ω∣ − 2 σ ε 2 x T Ω − 1 x 求偏导并令其为零
{ ∂ ℓ ∂ σ ε 2 = − n 2 σ ε 2 + x T Ω − 1 x 2 σ ε 4 = 0 ∂ ℓ ∂ β = − 1 2 ∂ ln ∣ Ω ∣ ∂ β − 1 2 σ ε 2 ∂ x T Ω − 1 x ∂ β = 0 \left\{ \begin{aligned}
\frac{\partial \ell}{\partial \sigma _\varepsilon ^2} & = -\frac{n}{2\sigma _\varepsilon ^2} + \frac{\boldsymbol x^T \Omega ^{-1} \boldsymbol x}{2 \sigma _\varepsilon ^4} = 0\\
\frac{\partial \ell}{\partial \boldsymbol \beta} & = -\frac 12 \frac{\partial \ln |\Omega|}{\partial \boldsymbol \beta} - \frac{1}{2 \sigma _\varepsilon ^2} \frac{\partial \boldsymbol x^T \Omega ^{-1} \boldsymbol x}{\partial \boldsymbol \beta} = 0
\end{aligned} \right. ⎩ ⎨ ⎧ ∂ σ ε 2 ∂ ℓ ∂ β ∂ ℓ = − 2 σ ε 2 n + 2 σ ε 4 x T Ω − 1 x = 0 = − 2 1 ∂ β ∂ ln ∣Ω∣ − 2 σ ε 2 1 ∂ β ∂ x T Ω − 1 x = 0 该方程组没有解析解, 甚至 ∂ ln ∣ Ω ∣ ∂ β \frac{\partial \ln |\Omega|}{\partial \boldsymbol \beta} ∂ β ∂ l n ∣Ω∣ ∂ x T Ω − 1 x ∂ β \frac{\partial \boldsymbol x^T \Omega ^{-1} \boldsymbol x}{\partial \boldsymbol \beta} ∂ β ∂ x T Ω − 1 x
例 若初值 x 0 x_0 x 0 A R ( 1 ) \mathrm{AR}(1) AR ( 1 ) X t = φ 0 + φ 1 X t − 1 + ε t X_t = \varphi _0 + \varphi _1 X_{t-1} + \varepsilon _t X t = φ 0 + φ 1 X t − 1 + ε t
L ( φ 0 , φ 1 , σ ε 2 ∣ x ) = p ( x t ∣ x t − 1 ) p ( x t − 1 ∣ x t − 2 ) ⋯ p ( x 2 ∣ x 1 ) p ( x 1 ∣ x 0 ) = 1 ( 2 π σ ε 2 ) n exp �� − ∑ i = 1 n ( x i − φ 0 − φ 1 x i − 1 ) 2 2 σ ε 2 \begin{aligned}
\mathcal L(\varphi _0, \varphi _1, \sigma _\varepsilon ^2 \mid \boldsymbol x) & = p(x_t \mid x_{t-1}) p(x_{t-1} \mid x_{t-2}) \cdots p(x_2 \mid x_1) p(x_1 \mid x_0)\\
& = \frac{1}{(\sqrt{2\pi \sigma _\varepsilon ^2})^n} \exp -\sum _{i=1}^n \frac{(x_i - \varphi _0 - \varphi _1 x_{i-1})^2}{2\sigma _\varepsilon ^2}
\end{aligned} L ( φ 0 , φ 1 , σ ε 2 ∣ x ) = p ( x t ∣ x t − 1 ) p ( x t − 1 ∣ x t − 2 ) ⋯ p ( x 2 ∣ x 1 ) p ( x 1 ∣ x 0 ) = ( 2 π σ ε 2 ) n 1 exp − i = 1 ∑ n 2 σ ε 2 ( x i − φ 0 − φ 1 x i − 1 ) 2 这与简单线性回归的极大似然估计相同. 它也等于简单线性回归的最小二乘估计.
极大似然估计充分利用观察值的信息, 估计精度高, 具有估计一致性、渐进正态性等优良统计性质, 但缺点是需要事先假定序列分布.
4.4.3 最小二乘估计
ARMA 模型的残差是
ε t = x t − φ 1 x t − 1 − ⋯ − φ p x t − p + θ 1 ε t − 1 + ⋯ + θ q + ε t − q \varepsilon _t = x_t - \varphi _1 x_{t-1} - \cdots - \varphi _p x_{t-p} + \theta _1 \varepsilon _{t-1} + \cdots + \theta _q + \varepsilon _{t-q} ε t = x t − φ 1 x t − 1 − ⋯ − φ p x t − p + θ 1 ε t − 1 + ⋯ + θ q + ε t − q 残差平方和为
Q = ∑ t = 1 n ε 2 Q = \sum _{t=1}^n \varepsilon ^2 Q = t = 1 ∑ n ε 2 由于随机扰动 ε t − 1 , ε t − 2 , … \varepsilon _{t-1}, \varepsilon _{t-2}, \dots ε t − 1 , ε t − 2 , … Q Q Q
A R ( p ) \mathrm{AR}(p) AR ( p ) A R ( p ) \mathrm{AR}(p) AR ( p )
X t = φ 0 + φ 1 X t − 1 + ⋯ + φ p X t − p + ε t X_t = \varphi _0 + \varphi _1 X_{t-1} + \cdots + \varphi _p X_{t-p} + \varepsilon _t X t = φ 0 + φ 1 X t − 1 + ⋯ + φ p X t − p + ε t 这是一个基本的多元线性回归问题, 可以直接使用多元线性回归的方法求解.
在实际中, 因为观测样本是有起点的, 所以残差一定可以展开成一个 t t t
ε t = x t − α 1 x t − 1 − ⋯ − α t − 1 x 1 \varepsilon _t = x_t - \alpha _1 x_{t-1} - \cdots - \alpha _{t-1} x_1 ε t = x t − α 1 x t − 1 − ⋯ − α t − 1 x 1 这就化为了一个标准的二次函数求最值问题, 称为条件最小二乘估计.
最小二乘估计充分利用了样本信息, 所以估计精度很高. 条件最小二乘估计是最常用的估计方法.
4.5 模型检验
4.5.1 模型的显著性检验
模型的的显著性检验等价于检验残差序列是否为白噪音. 因为若序列不是白噪音, 则说明模型对序列自相关性提取不充分, 从而应该重新选择��其它模型拟合. 模型显著性检验可以通过对残差序列进行 Ljung-Box 纯随机性检验完成.
4.5.2 参数的显著性检验
有时需要检验一个参数是否显著非零, 从而决定该阶系数是否要从拟合模型中剔除. 检验假设
H 0 : β i = 0 , H 1 : β i ≠ 0 H_0: \beta _i = 0, \qquad H_1: \beta _i \neq 0 H 0 : β i = 0 , H 1 : β i = 0 其中 1 ≤ i ≤ m 1 \leq i \leq m 1 ≤ i ≤ m m m m β i \beta _i β i
D β ^ i = ω j σ ε 2 , Ω = ( X T X ) − 1 = ( ω 1 ⋯ ∗ ⋮ ⋱ ⋮ ∗ ⋯ ω m ) \mathrm D \hat \beta _i = \omega _j \sigma _\varepsilon ^2, \qquad
\Omega = (X^TX)^{-1} = \begin{pmatrix}
\omega _1 & \cdots & *\\
\vdots & \ddots & \vdots\\
* & \cdots & \omega _m
\end{pmatrix} D β ^ i = ω j σ ε 2 , Ω = ( X T X ) − 1 = ω 1 ⋮ ∗ ⋯ ⋱ ⋯ ∗ ⋮ ω m 由于 σ ε 2 \sigma _\varepsilon ^2 σ ε 2
σ ^ ε 2 = Q n − m \hat \sigma _\varepsilon ^2 = \frac{Q}{n - m} σ ^ ε 2 = n − m Q 现在可以考虑 t t t
t = β ^ j ω j Q / ( n − m ) ∼ t ( n − m ) t = \frac{\hat \beta _j}{\sqrt{\omega _j Q / (n-m)}} \sim t(n-m) t = ω j Q / ( n − m ) β ^ j ∼ t ( n − m ) 4.6 模型优化
可能同时有很多显著的模型, 它们的拟合残差同时都是白噪音. 需要一个定量描述模型优度的指标.
时间序列的拟合实际上是一个双目标优化问题. 它有两个目标: 拟合优度最大, 待估参数个数最小. 但是该二优化目标是相互矛盾的: 因为参数越多, 拟合优度一定更大. 故应寻找一种让两个优化目标达到平衡的判断准则.
本问题首先对残差平方和 ∑ t ε t \sum_t\varepsilon_t ∑ t ε t t t t σ ^ ε 2 {\hat \sigma}_\varepsilon^2 σ ^ ε 2 p + q + 1 p+q+1 p + q + 1
A I C ( p , q ) = n ln σ ^ ε 2 + 2 ( p + q + 1 ) \mathrm{AIC}(p,q)=n\ln {\hat \sigma}_\varepsilon^2+2(p+q+1) AIC ( p , q ) = n ln σ ^ ε 2 + 2 ( p + q + 1 ) AIC 的值越小越好. AIC 的问题在于, ln σ ^ ε 2 \ln {\hat \sigma}_\varepsilon^2 ln σ ^ ε 2 n n n 2 2 2 n n n
B I C ( p , q ) = n ln σ ^ ε 2 + ln n ⋅ ( p + q + 1 ) \mathrm{BIC}(p,q)=n\ln {\hat \sigma}_\varepsilon^2+\ln n\cdot (p+q+1) BIC ( p , q ) = n ln σ ^ ε 2 + ln n ⋅ ( p + q + 1 ) AIC 偏向于预测, 会选择拟合度高的模型; BIC 偏向于拟合, 会选择参数较少的模型. 这两个信息准则各有优劣.
4.7 序列预测
4.7.1 线性预测
任意一个平稳 ARMA 模型有逆转形式
X t = − I 1 X t − 1 − I 2 X t − 2 − ⋯ − I t − 1 X 1 + ε t X_t = -I_1 X_{t-1} - I_2 X_{t-2} - \cdots - I_{t-1} X_1 + \varepsilon _t X t = − I 1 X t − 1 − I 2 X t − 2 − ⋯ − I t − 1 X 1 + ε t 忽略白噪音项后, 可以得到未来时间序列的点估计
x ^ t + 1 = − I 1 x t − I 2 x t − 1 − ⋯ , x ^ t + 2 = − I 1 x ^ t + 1 − I 2 x t − ⋯ \hat x_{t+1} = -I_1 x_t - I_2 x_{t-1} - \cdots, \qquad
\hat x_{t+2} = -I_1 \hat x_{t+1} - I_2 x_t - \cdots x ^ t + 1 = − I 1 x t − I 2 x t − 1 − ⋯ , x ^ t + 2 = − I 1 x ^ t + 1 − I 2 x t − ⋯ x ^ t + 2 \hat x_{t+2} x ^ t + 2 x ^ t + 1 \hat x_{t+1} x ^ t + 1
x ^ t + 2 = ( I 1 2 − I 2 ) x t + ( I 1 I 2 − I 3 ) x t − 1 + ⋯ \hat x_{t+2} = (I_1^2 - I_2) x_t + (I_1I_2 - I_3) x_{t-1} + \cdots x ^ t + 2 = ( I 1 2 − I 2 ) x t + ( I 1 I 2 − I 3 ) x t − 1 + ⋯ 4.7.2 预测方差最小原则
预测方差最小原则希望最小化预测方差. 对于 k k k e t + k e_{t+k} e t + k
e t + k : = x t + k − x ^ t + k , D e t + k = min e_{t+k} := x_{t+k} - \hat x_{t+k}, \qquad
\mathrm De_{t+k} = \min e t + k := x t + k − x ^ t + k , D e t + k = min 考虑传递形式 x t + k = ε t + k + G 1 ε t + k − 1 + ⋯ x_{t+k} = \varepsilon _{t+k} + G_1 \varepsilon _{t+k-1} + \cdots x t + k = ε t + k + G 1 ε t + k − 1 + ⋯ x ^ t + k \hat x_{t+k} x ^ t + k { x t , x t − 1 , … } \{x_t, x_{t-1}, \dots\} { x t , x t − 1 , … }
x ^ t + k = D 0 x t + D 1 x t − 1 + D 2 x t − 2 + ⋯ = D 0 ( ε t + G 1 ε t − 1 + G 2 ε t − 2 + ⋯ ) + D 1 ( ε t − 1 + G 1 ε t − 2 + ⋯ ) + D 2 ( ε t − 2 + ⋯ ) = D 0 ⏟ W 0 ε t + ( D 0 G 1 + D 1 ⏟ W 1 ) ε t − 1 + ( D 0 G 2 + D 1 G 1 + D 2 ⏟ W 2 ) ε t − 2 + ⋯ = : W 0 ε t + W 1 ε t − 1 + W 2 ε t − 2 + ⋯ \begin{aligned}
\hat x_{t+k} & = D_0 x_t + D_1 x_{t-1} + D_2 x_{t-2} + \cdots\\
& = D_0(\varepsilon _t + G_1 \varepsilon _{t-1} + G_2 \varepsilon _{t-2} + \cdots) + D_1(\varepsilon _{t-1} + G_1 \varepsilon _{t-2} + \cdots) + D_2(\varepsilon _{t-2} + \cdots)\\
& = \underbrace{D_0}_{W_0} \varepsilon _t + (\underbrace{D_0G_1 + D_1}_{W_1}) \varepsilon _{t-1} + (\underbrace{D_0G_2 + D_1G_1 + D_2}_{W_2}) \varepsilon _{t-2} + \cdots\\
& =: W_0 \varepsilon_t + W_1 \varepsilon_{t-1} + W_2 \varepsilon _{t-2} + \cdots
\end{aligned} x ^ t + k = D 0 x t + D 1 x t − 1 + D 2 x t − 2 + ⋯ = D 0 ( ε t + G 1 ε t − 1 + G 2 ε t − 2 + ⋯ ) + D 1 ( ε t − 1 + G 1 ε t − 2 + ⋯ ) + D 2 ( ε t − 2 + ⋯ ) = W 0 D 0 ε t + ( W 1 D 0 G 1 + D 1 ) ε t − 1 + ( W 2 D 0 G 2 + D 1 G 1 + D 2 ) ε t − 2 + ⋯ =: W 0 ε t + W 1 ε t − 1 + W 2 ε t − 2 + ⋯ 预测误差是
e t + k = x t + k − x ^ t + k = ( ε t + k + G 1 ε t + k − 1 + ⋯ + G k ε t + ⋯ ) − ( W 0 ε t + W 1 ε t − 1 + ⋯ ) = ( ε t + k + G 1 ε t + k − 1 + ⋯ + G k − 1 ε t + 1 ) + ( G k − W 0 ) ε t + ( G k + 1 − W 1 ) ε t − 1 + ⋯ \begin{aligned}
e_{t+k} & = x_{t+k} - \hat x_{t+k}\\
& = (\varepsilon _{t+k} + G_1 \varepsilon _{t+k-1} + \cdots + G_k \varepsilon _t + \cdots) - (W_0 \varepsilon_t + W_1 \varepsilon_{t-1} + \cdots)\\
& = (\varepsilon _{t+k} + G_1 \varepsilon _{t+k-1} + \cdots + G_{k-1} \varepsilon _{t+1}) + (G_k - W_0) \varepsilon _t + (G_{k+1} - W_1) \varepsilon _{t-1} + \cdots
\end{aligned} e t + k = x t + k − x ^ t + k = ( ε t + k + G 1 ε t + k − 1 + ⋯ + G k ε t + ⋯ ) − ( W 0 ε t + W 1 ε t − 1 + ⋯ ) = ( ε t + k + G 1 ε t + k − 1 + ⋯ + G k − 1 ε t + 1 ) + ( G k − W 0 ) ε t + ( G k + 1 − W 1 ) ε t − 1 + ⋯ 它的方差是
D e t + k = ( ( 1 + G 1 + ⋯ + G k − 1 ) + ( G k − W 0 ) + ( G k + 1 − W 1 ) + ⋯ ) σ ε 2 \mathrm De_{t+k} = \Big((1 + G_1 + \cdots + G_{k-1}) + (G_k - W_0) + (G_{k+1} - W_1) + \cdots \Big) \sigma _\varepsilon ^2 D e t + k = ( ( 1 + G 1 + ⋯ + G k − 1 ) + ( G k − W 0 ) + ( G k + 1 − W 1 ) + ⋯ ) σ ε 2 要使方差最小, 我们令
G k = W 0 , G k + 1 = W 1 , ⋯ G_k = W_0, \qquad
G_{k+1} = W_1, \qquad
\cdots G k = W 0 , G k + 1 = W 1 , ⋯ 所以预测值是
x ^ t + k = G k ε t + G k + 1 ε t − 1 + ⋯ \hat x_{t+k} = G_k \varepsilon _t + G_{k+1} \varepsilon _{t-1} + \cdots x ^ t + k = G k ε t + G k + 1 ε t − 1 + ⋯ 预测误差的均值和方差是
E e t + k = 0 , D e t + k = ( 1 + G 1 + ⋯ + G k − 1 ) σ ε 2 \mathrm Ee_{t+k} = 0, \qquad
\mathrm De_{t+k} = (1 + G_1 + \cdots + G_{k-1}) \sigma _\varepsilon ^2 E e t + k = 0 , D e t + k = ( 1 + G 1 + ⋯ + G k − 1 ) σ ε 2 4.7.3 线性最小方差预测的性质
AR 模型预测 A R ( p ) \mathrm{AR}(p) AR ( p ) k k k
x ^ t + k = φ 0 + φ 1 x t + k − 1 + ⋯ + φ p x t + k − p \hat x_{t+k} = \varphi _0 + \varphi _1 x_{t+k-1} + \cdots + \varphi _p x_{t+k-p} x ^ t + k = φ 0 + φ 1 x t + k − 1 + ⋯ + φ p x t + k − p 其中 t + k − p ≥ t t+k-p \geq t t + k − p ≥ t
D e t + k = ( 1 + G 1 2 + ⋯ + G k − 1 2 ) σ ε 2 \mathrm De_{t+k} = (1 + G_1^2 + \cdots + G_{k-1}^2) \sigma _\varepsilon ^2 D e t + k = ( 1 + G 1 2 + ⋯ + G k − 1 2 ) σ ε 2 MA 模型预测 M A ( q ) \mathrm{MA}(q) MA ( q ) k k k
x ^ t + k = { μ − θ k ε t − θ k + 1 ε t − 1 + ⋯ + θ q ε t + k − q , k ≤ q μ , k > q \hat x_{t+k} = \begin{cases}
\mu - \theta _k \varepsilon _t - \theta _{k+1} \varepsilon _{t-1} + \cdots + \theta _q \varepsilon _{t+k-q}, & k \leq q\\
\mu, & k > q
\end{cases} x ^ t + k = { μ − θ k ε t − θ k + 1 ε t − 1 + ⋯ + θ q ε t + k − q , μ , k ≤ q k > q 其中 ε i \varepsilon _i ε i x i x_i x i M A ( q ) \mathrm{MA}(q) MA ( q ) q q q k k k q − k + 1 q-k+1 q − k + 1 q q q
D e t + k = { ( 1 + θ 1 2 + ⋯ + θ k − 1 2 ) σ ε 2 , k ≤ q ( 1 + θ 1 2 + ⋯ + θ q 2 ) σ ε 2 , k > q \mathrm De_{t+k} = \begin{cases}
(1 + \theta _1^2 + \cdots + \theta _{k-1}^2) \sigma _\varepsilon ^2, & k \leq q\\
(1 + \theta _1^2 + \cdots + \theta _q^2) \sigma _\varepsilon ^2, & k > q
\end{cases} D e t + k = { ( 1 + θ 1 2 + ⋯ + θ k − 1 2 ) σ ε 2 , ( 1 + θ 1 2 + ⋯ + θ q 2 ) σ ε 2 , k ≤ q k > q ARMA 模型预测 A R M A ( p , q ) \mathrm{ARMA}(p, q) ARMA ( p , q ) k k k
x ^ t + k = { φ 0 + φ 1 x t + k − 1 + ⋯ + φ p x t + k − p − θ k ε t − θ k + 1 ε t − 1 + ⋯ + θ q ε t + k − q , k ≤ q φ 0 + φ 1 x t + k − 1 + ⋯ + φ p x t + k − p , k > q \hat x_{t+k} = \begin{cases}
\varphi _0 + \varphi _1 x_{t+k-1} + \cdots + \varphi _p x_{t+k-p} - \theta _k \varepsilon _t - \theta _{k+1} \varepsilon _{t-1} + \cdots + \theta _q \varepsilon _{t+k-q}, & k \leq q\\
\varphi _0 + \varphi _1 x_{t+k-1} + \cdots + \varphi _p x_{t+k-p}, & k > q
\end{cases} x ^ t + k = { φ 0 + φ 1 x t + k − 1 + ⋯ + φ p x t + k − p − θ k ε t − θ k + 1 ε t − 1 + ⋯ + θ q ε t + k − q , φ 0 + φ 1 x t + k − 1 + ⋯ + φ p x t + k − p , k ≤ q k > q 其中 t + k − p ≥ t t+k-p \geq t t + k − p ≥ t ε i \varepsilon _i ε i x i x_i x i
D e t + k = ( 1 + G 1 2 + ⋯ + G k − 1 2 ) σ ε 2 \mathrm De_{t+k} = (1 + G_1^2 + \cdots + G_{k-1}^2) \sigma _\varepsilon ^2 D e t + k = ( 1 + G 1 2 + ⋯ + G k − 1 2 ) σ ε 2 4.7.4 修正预测
假设在已知旧信息 { x t } \{x_t\} { x t } x t + 1 x_{t+1} x t + 1
x ^ t + k ← G k − 1 ε t + 1 + x ^ t + k \hat x_{t+k} \gets G_{k-1} \varepsilon _{t+1} + \hat x_{t+k} x ^ t + k ← G k − 1 ε t + 1 + x ^ t + k 其中 ε t + 1 \varepsilon _{t+1} ε t + 1 x t + 1 x_{t+1} x t + 1
D e t + k ← D e t + k − G k − 1 2 σ ε 2 \mathrm De_{t+k} \gets \mathrm De_{t+k} - G_{k-1}^2 \sigma _\varepsilon ^2 D e t + k ← D e t + k − G k − 1 2 σ ε 2 假设在已知旧信息 { x t } \{x_t\} { x t } { x t + p } \{x_{t+p}\} { x t + p }
x ^ t + k ← G k − p ε t + p + ⋯ + G k − 1 ε t + 1 + x ^ t + k \hat x_{t+k} \gets G_{k-p} \varepsilon _{t+p} + \cdots + G_{k-1} \varepsilon _{t+1} + \hat x_{t+k} x ^ t + k ← G k − p ε t + p + ⋯ + G k − 1 ε t + 1 + x ^ t + k 修正后的预测误差的方差为
D e t + k ← D e t + k − ( G k − 1 2 + ⋯ + G k − p 2 ) σ ε 2 \mathrm De_{t+k} \gets \mathrm De_{t+k} - (G_{k-1}^2 + \cdots + G_{k-p}^2) \sigma _\varepsilon ^2 D e t + k ← D e t + k − ( G k − 1 2 + ⋯ + G k − p 2 ) σ ε 2