有理函数的不定积分方法
摘 要 在实际应用的场合中, 绝大部分函数的不定积分其实是积不出的, 所以积得出的那一部分函数就显得尤为珍贵. 本文旨在介绍一类已经被完全解决了的问题: 形如 P(x)/Q(x) 的有理分式函数的积分方法. 其中 P(x) 和 Q(x) 为关于 x 的多项式.
1 多项式除法
真分式与假分式 分子次数小于分母的有理分式称为真分式, 否则称为假分式.
假分式的分解 如同假分数可以分解为一个整数与一个真分数之和, 假分式也可��以分解为一个分式与一个真分式之和. 例如
x+1x3+x+3=x2−x+2+x+11
假分式的分解通过多项式除法完成. 多项式除法与数的除法是一样的, 仅仅是数的各数位换成了多项式的各项.
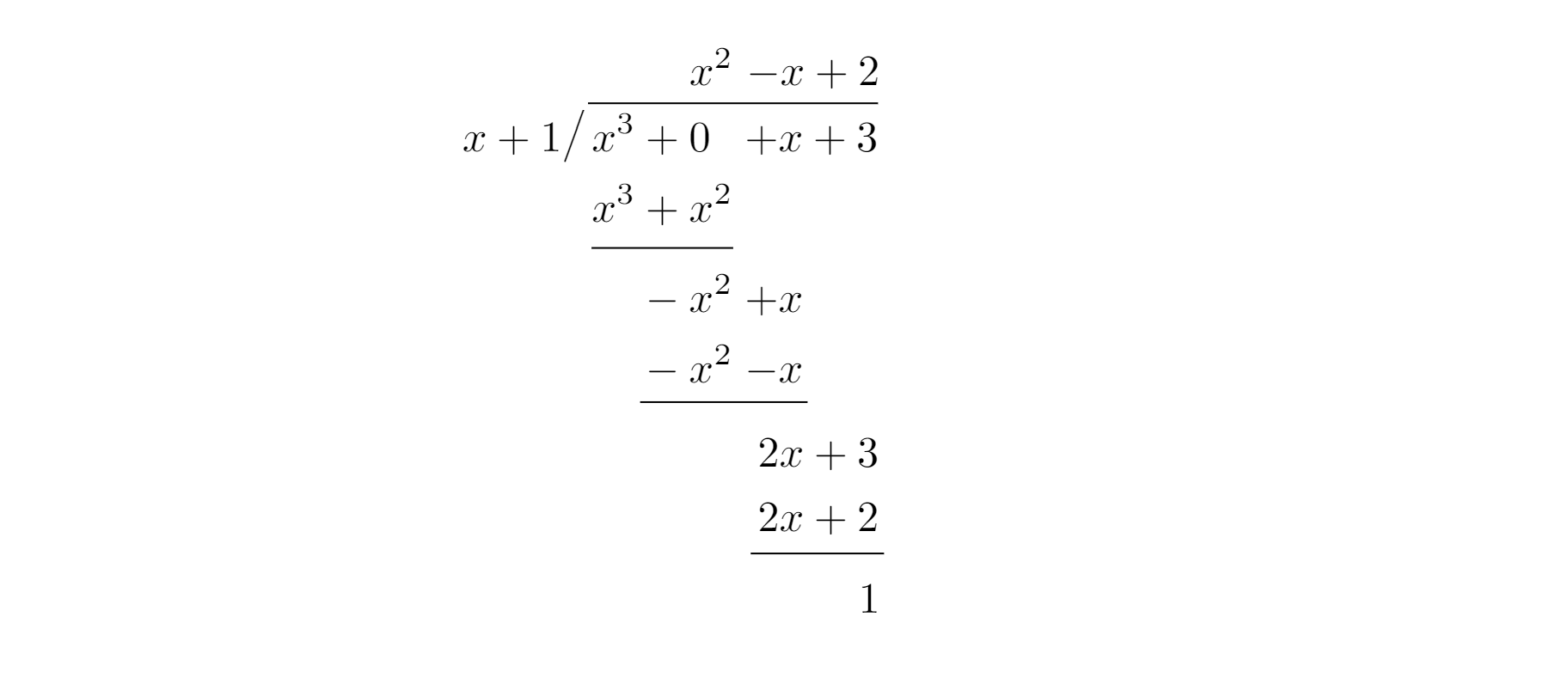 在上图所示的竖式中, 被除数位置为被除式, 左边是除式, 顶部为商式, 右下为余式. 该竖式将被除式分解为了
在上图所示的竖式中, 被除数位置为被除式, 左边是除式, 顶部为商式, 右下为余式. 该竖式将被除式分解为了
除式被除式=商式+除式余式
2 真分式的部分分式分解
部分分式 部分分式包括两类, 一类分母是一次项的幂、分子是常数, 一类分母是二次项的幂、分子是一次项. 即
(x−a)kAand(x2+px+q)kMx+N
其中 k=1,2,⋯.
实数系内多项式的因式分解定理 实数范围内, 任意一个多项式都可以分解为若干个一次多项式 (x−a) 和若干个二次不可约多项式 (x2+px+q),p2−4q<0 的乘积的形式.
例 x5+x4−2x3−x2−x+2=(x−1)2(x+2)(x2+x+1)
注 多项式的因式分解其实是求根的过程. 由于 n 次多项式必有 n 个根 (可能是复根), 且复根必成对出现, 故每一个实根 x=a 对应一个一次多项式 (x−a), 每一对复根 x=u±iv 对应一个二次不可约多项式 (x−u−iv)(x−u+iv).
部分分式分解定理 任意一个有理分式函数都可以分解为部分分式之和的形式.
下面介绍部分分式分解的步骤. 首先将部分分式的分母 Q(x) 在实数范围内作彻底的因式分解 (即前述所提到的若干一次多项式和若干二次不可约多项式之积).
因式中的一次多项式
- 若因式中有一个 (x−a), 则分解后的式子中应有一个 x−aA, 其中 A 是待定系数.
- 若因式中有一个 (x−a)2, 则分解后的式子中应有一个 x−aA+(x−a)2B, 其中 A,B 是待定系数.
- 若因式中有一个 (x−a)3, 则分解后的式子中应有一个 x−aA+(x−a)2B+(x−a)3C, 其中 A,B,C 是待定系数.
- 以此类推
因式中的二次不可约多项式
- 若因式中有一个 (x2+px+q), 则分解后的式子中应有一个 x+px+qMx+N, 其中 M,N 是待定系数.
- 若因式中有一个 (x2+px+q)2, 则分解后的式子中应有一个 x+px+qMx+N+(x+px+q)2Sx+T, 其中 M,N,S,T 是待定系数.
- 若因式中有一个 (x2+px+q)3, 则分解后的式子中应有一个 x+px+qMx+N+(x+px+q)2Sx+T+(x+px+q)3Ux+V, 其中 M,N,S,T,U,V 是待定系数.
- 以此类推
例 因式分解的结果是 (x−1)2(x+2)(x2+x+1), 故部分分式分解的结果应该是
x−1A+(x−1)2B+x+2C+x2+x+1Dx+E
其中 A,B,C,D,E 是待定系数. 从上述规则可以看出, 待定系数的数量与原多项式的次数应该是一样的.
将上述分解式通分后与原分式对应系数比较, 即可求得各待定系数的值.
例 作部分分式分解 x2−11.
x2−11=(x−1)(x+1)1=x−1A+x+1B=x2−1(A+B)x+(A−B)
上式第一式与最后一式对应系数相等, 列出方程并求解
{01=A+B=A−B⟹{AB=1/2=−1/2
故
x2−11=x−11/2+x+1−1/2
例 作部分分式分解 x5+x4−2x3−x2−x+2x3−2x.
解
===x5+x4−2x3−x2−x+2x3−2x(x−1)2(x+2)(x2+x+1)x3−2xx−1A+(x−1)2B+x+2C+x2+x+1Dx+E(x−1)2(x+2)(x2+x+1)(A+C+D)x4+(2A+B−C+E)x3+(3B−3D)x2+(−A+3B−C+2D−3E)x+(−2A+2B+C+2E)
上式第二行与第四行对应系数相等, 列出方程并求解
⎩⎨⎧010−20=A+C+D=2A+B−C+E=3B−3D=−A+3B−C+2D−3E=−2A+2B+C+2E⟹⎩⎨⎧ABCDE=−1=1=0=1=2
故
x5+x4−2x3−x2−x+2x3−2x=x−1−1+(x−1)21+x2+x+1x+2
3 部分分式的不定积分
x−a1 的不定积分
∫x−adx=ln∣x−a∣+C
(x−a)k1 的不定积分
∫(x−a)kdx=∫(x−a)kd(x−a)=(1−k)(x−a)k−11+C
对于二次不可约多项式 (x2+px+q), 为运算简便, 一般先将其配方为 (x−a)2+r2 后研究.
x2+px+qx 的不定积分
∫x2+px+qxdx=配方∫(x−a)2+r2xdx=∫(x−a)2+r2(x−a)dx+∫(x−a)2+r2adx=21ln((x−a)2+r2)+∫(x−a)2+r2adx
(x2+px+q)kx 的不定积分
∫(x2+px+q)kxdx=配方∫((x−a)2+r2)kxdx=∫((x−a)2+r2)k(x−a)dx+∫((x−a)2+r2)kadx=2(1−k)((x−a)2+r2)k−11+∫((x−a)2+r2)kadx
x2+px+q1 的不定积分
∫x2+px+qdx=配方∫(x−a)2+r2dx=r1∫(rx−a)2+1d(rx−a)=r1arctanrx−a+C
(x2+px+q)k1 的不定积分
Ik=∫(x2+px+q)kdx=配方∫((x−a)2+r2)kdx=t:=x−a∫(t2+r2)kdx=r21∫(t2+r2)k(t2+r2)−t2=r21Ik−1−r21∫(t2+r2)kt2dt
其中
∫(t2+r2)kt2dt=凑微分21∫(t2+r2)ktd(t2+r2)=21∫t(t2+r2)−kd(t2+r2)=凑微分21∫td1−k(t2+r2)1−k=2(1−k)1∫td(t2+r2)k−11=分部积分2(1−k)1((t2+r2)k−1t−Ik−1)
回代, 得
Ik=r21Ik−1−r21∫(t2+r2)kt2dt=r21Ik−1+2r2(k−1)1((t2+r2)k−1t−Ik−1)=2r2(k−1)2k−3Ik−1+2r2(k−1)(t2+r2)k−1t=回代2r2(k−1)2k−3Ik−1+2r2(k−1)((x−a)2+r2)k−1x−a
上式给出了 Ik 到 Ik−1 的递推关系. 多次运用该式, 直到归结为 I1 即可.
至此, 有理分式函数的不定积分求解已经全部完成. 所有有理分式函数的不定积分均是初等函数.
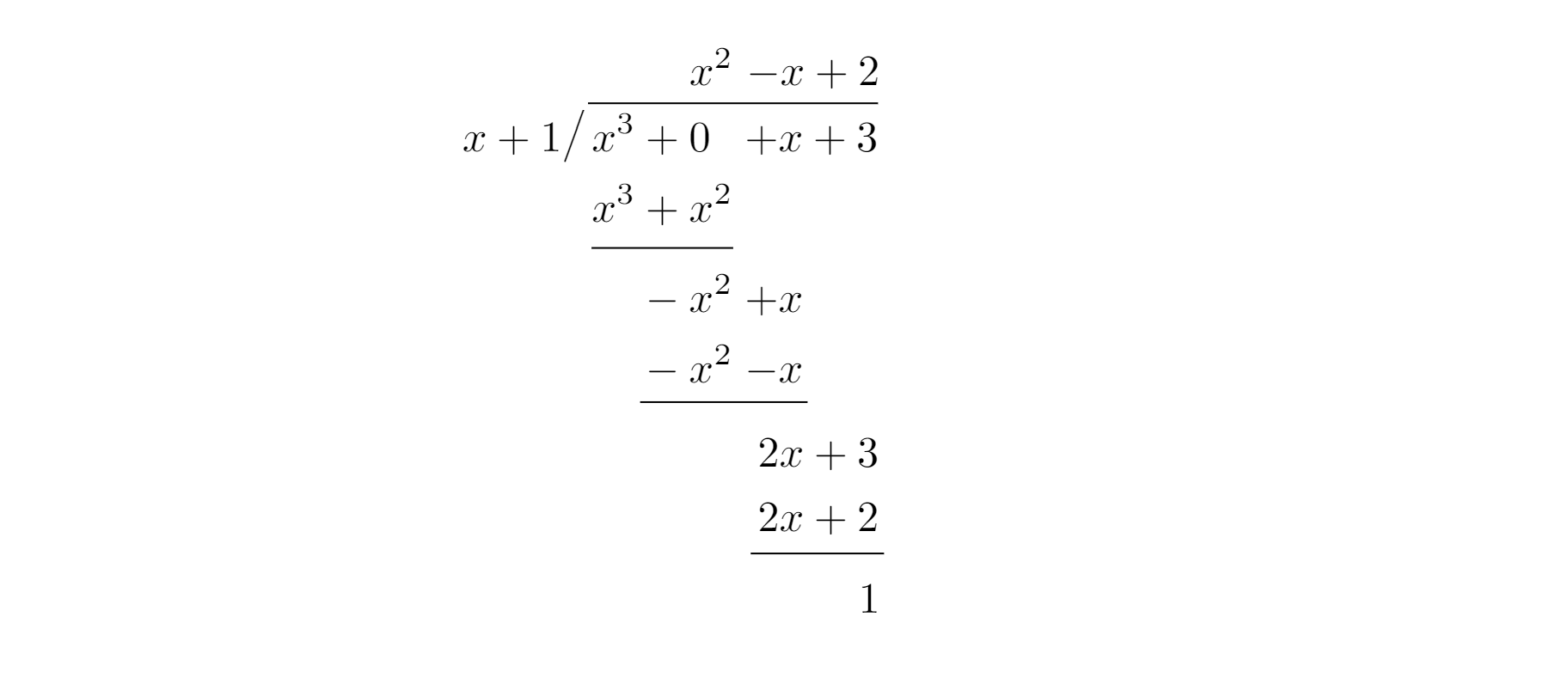 在上图所示的竖式中, 被除数位置为被除式, 左边是除式, 顶部为商式, 右下为余式. 该竖式将被除式分解为了
在上图所示的竖式中, 被除数位置为被除式, 左边是除式, 顶部为商式, 右下为余式. 该竖式将被除式分解为了